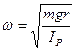|
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 15 การเคลื่อนที่แบบสั่น
เนื้อหาประกอบด้วย
15.1 แรงบนสปริง – กฎของฮุค (Hooke’s Rule)
15.2 การเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
15.3 ความสัมพันธ์กับการเคลื่อนที่แบบวงกลม
15.4 แรงและพลังงานในการเคลื่อนที่แบบซิมเปิลฮาร์โมนิกอย่างง่าย
15.5 รูปแบบต่าง ๆ ของการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
ในบทนี้จะศึกษาเกี่ยวกับการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
(Simple
Harmonic Moion, SHM) ตัวอย่าง เช่น การสั่นของมวลที่ติดปลายสปริง
ซึ่งสมการการเคลื่อนที่เราสามารถหาได้โดยการประยุกต์ใช้กฎต่าง ๆ
ที่ได้ศึกษามาก่อนหน้านี้ เช่นการประยุกต์ใช้กฎข้อสองของนิวตันเพื่อหาสมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
จะได้สมการที่ ตำแหน่งเป็นฟังชั่นของเวลา ![]() ; ความเร็วเป็น
ฟังชั่นของเวลา
; ความเร็วเป็น
ฟังชั่นของเวลา ![]() ;
ความเร่งเป็นฟังชั่นของเวลา
;
ความเร่งเป็นฟังชั่นของเวลา ![]() หรือ
ความเร็วเป็นฟังก์ชั่นของตำแหน่ง
หรือ
ความเร็วเป็นฟังก์ชั่นของตำแหน่ง ![]() และ
ความเร่งเป็นฟังชั่นของตำแหน่ง
และ
ความเร่งเป็นฟังชั่นของตำแหน่ง ![]()
15.1 แรงบนสปริง – กฎของฮุค
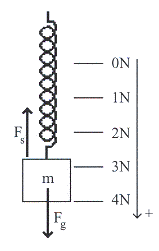 เมื่อนำมวลมาแขวนที่ปลายสปริงและอยู่ในสภาพสมดุล จากกฎข้อสองของนิวตัน
เมื่อนำมวลมาแขวนที่ปลายสปริงและอยู่ในสภาพสมดุล จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อเพิ่มน้ำหนักจนทำให้สปริงยืดออก แรงที่กระทำต่อสปริง
(แรงเนื่องจากวัตถุมวล ![]() ;
; ![]() ) จะเป็นสัดส่วนโดยตรงกับระยะยืดของสปริง
และมีทิศตรงข้ามกับแรงสปริง
) จะเป็นสัดส่วนโดยตรงกับระยะยืดของสปริง
และมีทิศตรงข้ามกับแรงสปริง ![]() ดังรูปที่ 15.1
ดังรูปที่ 15.1
![]() =
= ![]()
เมื่อ ![]() เรียกว่าค่าคงที่ของสปริง
(spring constant)
เรียกว่าค่าคงที่ของสปริง
(spring constant)
กฎของฮุค : ![]() =
= ![]()
รูปที่ 15.1
ตัวอย่างที่
15.1
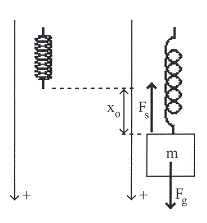
จงหาค่าคงที่ของสปริง เมื่อนำมวล ![]() มาแขวนที่ปลายสปริงแล้วทำให้สปริงยืดออกจากตำแหน่งสมดุลเดิมเป็นระยะ
มาแขวนที่ปลายสปริงแล้วทำให้สปริงยืดออกจากตำแหน่งสมดุลเดิมเป็นระยะ
![]() ดังรูปที่
15.2
ดังรูปที่
15.2
 วิธีทำ
จากกฎข้อสองของนิวตัน
วิธีทำ
จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
จากกฎของฮุคและแทนค่าแรงเนื่องจากน้ำหนักของมวล
![]() =
= ![]()
เมื่อ
![]() คือระยะยืดของสปริง
จากนั้นแทนค่าต่าง ๆ ลงในสมการ
คือระยะยืดของสปริง
จากนั้นแทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
=
![]()
รูปที่ 15.2 = ![]()
15.2 การเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
การหาสมการการเคลื่อนที่ของวัตถุแบบซิมเปิลฮาร์โมนิก
สามารถประยุกต์ใช้กฎข้อสองของนิวตันโดยมีความเร่งเข้าเกี่ยวข้อง
(เนื่องจากวัตถุมีการเคลื่อนที่) ซึ่งความเร็วและความเร่งสามารถหาได้จากสมการ
ตำแหน่งเป็นฟังก์ชั่นของเวลา ![]()
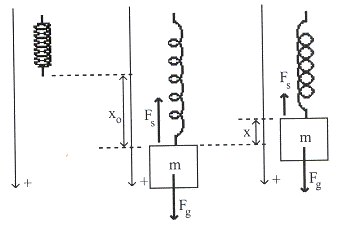
(ก) (ข) (ค)
รูปที่ 15.3
พิจารณาการเคลื่อนที่แบบแบบซิมเปิลฮาร์โมนิก
เมื่อระบบไม่สมดุลเดิมสปริงอยู่ในตำแหน่งสมดุลดังรูปที่ 15.3 ก. จากนั้นนำมวล ![]() มาแขวนที่ปลายสปริงทำให้สปริงยืดออกเป็นระยะ
มาแขวนที่ปลายสปริงทำให้สปริงยืดออกเป็นระยะ
![]() ดังรูปที่
15.3 ข. ระบบจะอยู่ในตำแหน่งสมดุลอีกครั้ง จากนั้นยกมวล
ดังรูปที่
15.3 ข. ระบบจะอยู่ในตำแหน่งสมดุลอีกครั้ง จากนั้นยกมวล ![]() ขึ้นเป็นระยะ
ขึ้นเป็นระยะ ![]() เหนือตำแหน่งสมดุลดังรูปที่
15.3 ค. แล้วปล่อยให้สปริงสั่น
เหนือตำแหน่งสมดุลดังรูปที่
15.3 ค. แล้วปล่อยให้สปริงสั่น
จากกฎข้อสองของนิวตัน
เมื่อมวล ![]() เคลื่อนที่
(ระบบไม่สมดุล)
เคลื่อนที่
(ระบบไม่สมดุล)
![]() =
= ![]()
![]() =
= ![]()
เมื่อสปริงยืดออกเป็นระยะ
![]() อาศัยกฎของฮุค
อาศัยกฎของฮุค
![]() =
= ![]()
จากกฎข้อสองของนิวตันเมื่อมวล
![]() อยู่ในตำแหน่งสมดุลมวล
อยู่ในตำแหน่งสมดุลมวล
![]() อยู่นิ่ง
อยู่นิ่ง
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่า
![]() ลงในสมการด้านบน
(เมื่อระบบไม่สมดุล) จะได้
ลงในสมการด้านบน
(เมื่อระบบไม่สมดุล) จะได้
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
นั่นคือความเร่งจะเป็นสัดส่วนโดยตรงกับการกระจัดแต่มีทิศทางตรงกันข้าม เพื่อความสะดวกกำหนดให้
![]() =
= ![]()
เขียนสมการใหม่ได้เป็น
![]() =
= ![]()
จากความสัมพันธ์ระหว่างความเร็วและความเร่ง โดยอาศัยกฎลูกโซ่จะได้
![]() =
= ![]() =
= ![]()
= ![]()
จะได้ ![]() =
= ![]()
![]() =
= ![]()
อินทิเกรตทั้งสองข้าง
โดยมี limit
ของตำแหน่งจาก ![]() ไปยังตำแหน่ง
ไปยังตำแหน่ง ![]() ใด ๆ
ใด ๆ
![]() =
= ![]()
สาเหตุที่ใช้ตำแหน่งตอนแรกเป็น ![]() เนื่องจากที่ตำแหน่งนี้ความเร็วจะเป็นศูนย์
ให้ปล่อยมวลที่ระยะ
เนื่องจากที่ตำแหน่งนี้ความเร็วจะเป็นศูนย์
ให้ปล่อยมวลที่ระยะ ![]() เมื่อ
เมื่อ ![]() เรียกว่า “แอมปลิจูด” จะได้
เรียกว่า “แอมปลิจูด” จะได้
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
นั่นคือความเร็วจะเป็นฟังก์ชั่นของตำแหน่ง
![]() =
= ![]()
การหาสมการเมื่อ ตำแหน่งเป็นฟังก์ชั่นของเวลาเวลา โดยอาศัยเงื่อนไขของความเร็ว
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
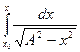 =
= ![]()
ในกรณีนี้
![]() แต่โดยทั่วไปจะมีค่าเท่าใดก็ได้แต่ต้องน้อยกว่าหรือเท่ากับ
แต่โดยทั่วไปจะมีค่าเท่าใดก็ได้แต่ต้องน้อยกว่าหรือเท่ากับ
![]()
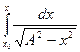 =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อเทอมที่สองทางซ้ายมือเป็นค่าคงที่ ขึ้นอยู่กับตำแหน่งเริ่มต้นของมวล เราเรียกว่ามุมเฟสเมื่อ
![]() =
= ![]()
จะได้
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
จะได้ตำแหน่งเป็นฟังชั่นของเวลา
![]() =
= ![]()
การหาสมการ ความเร็วเป็นฟังชั่นของเวลา โดยอาศัยเงื่อนไขของความเร็ว
![]() =
= ![]()
![]() =
= ![]()
จะได้ความเร็วเป็นฟังชั่นของเวลา
![]() =
= ![]()
จากความสัมพันธ์ระหว่างความเร็วและความเร่ง โดยหาอนุพันธ์ของความเร็วเทียบกับเวลา
![]() =
= ![]()
= ![]()
จะได้ความเร่งเป็นฟังชั่นของเวลา
![]() =
= ![]()
สรุป
เริ่มต้นใช้กฎข้อของของนิวตัน
โดยพิจารณาแรงที่เกิดจากวัตถุมวล ![]() กระทำที่ปลายสปริง
แล้วทำให้วัตถุมีความเร่ง จากนั้นอาศัยความสัมพันธ์ระหว่างความเร็วกับความเร่ง จะได้สมการการเคลื่อนที่
ของตำแหน่ง ความเร็ว และความเร่ง ดังนี้
กระทำที่ปลายสปริง
แล้วทำให้วัตถุมีความเร่ง จากนั้นอาศัยความสัมพันธ์ระหว่างความเร็วกับความเร่ง จะได้สมการการเคลื่อนที่
ของตำแหน่ง ความเร็ว และความเร่ง ดังนี้
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อ
![]()
![]() คือแอมปลิจูด ;
คือแอมปลิจูด ; ![]() คือมุมเฟส ;
คือมุมเฟส ;
![]() คือควาเร็วเชิงมุม
คือควาเร็วเชิงมุม
ความถี่เชิงมุมของวัตถุมวล
![]() ที่ติดปลายสปริงคือ
ที่ติดปลายสปริงคือ
![]() =
= ![]()
ค่า sines และค่า cosines บอกให้เราทราบว่าวัตถุเคลื่อนที่แบบสั่น หรือแบบฮาร์โมนิก ที่ใช้คำว่าอย่างง่ายเนื่องจากเคลื่อนที่พื้นฐานแบบฮาร์โมนิกมีหลายรูปแบบ (ซึ่งมีความยุ่งยากในการหา) ความเร่งจะเป็นสัดส่วนโดยตรงกับการกระจัดแต่ทิศตรงข้าม
ตัวอย่างที่
15.2
จากตัวอย่างที่ 15.1 เมื่อยกมวล ![]() ขึ้น
ขึ้น ![]() แล้วปล่อยจากจุดหยุดนิ่งจงคำนวณหา ก.
ความถี่เชิงมุม ข. แอมปลิจูด ง. มุมเฟส
แล้วปล่อยจากจุดหยุดนิ่งจงคำนวณหา ก.
ความถี่เชิงมุม ข. แอมปลิจูด ง. มุมเฟส
วิธีทำ ก. ความถี่เชิงมุมของสปริงคือ
![]() =
= ![]()
= 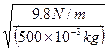
= ![]()
ข.
แอมปลิจูดคือการกระจัดสูงสุด ![]()
ค. เราทราบว่า ![]() เมื่อ
เมื่อ ![]() จาก
จาก
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
ตัวอย่างที่
15.3
จากตัวอย่างที่ 15.2 จงหาเวลาและความเร็วเมื่อมวล ![]() เคลื่อนที่มาถึงตำแหน่งสมดุล
เคลื่อนที่มาถึงตำแหน่งสมดุล
วิธีทำ
ต้องการหาเวลาเมื่อกำหนดตำแหน่งมาให้ ที่ตำแหน่งสมดุล ![]() จากสมการตำแหน่งเป็นฟังก์ชั่นของเวลา
จากสมการตำแหน่งเป็นฟังก์ชั่นของเวลา
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]()
จากตัวอย่างที่
15.2 เมื่อ ![]() จะได้
จะได้
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
จากนั้นในสมการความเร็วที่เป็นฟังก์ชั่นของเวลา
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
ความเร็วเป็นลบ
![]() แสดงว่ามวล
แสดงว่ามวล
![]() เคลื่อนที่ลง
เคลื่อนที่ลง
ตัวอย่างที่ 15.4 จงหาสมการของ
ก. ความเร็วสูงสุด
ข. ความเร่งสูงสุด
ง. คาบของการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก ในเทอมของความถี่เชิงมุมและอัมปลิจูด
จากสมการที่ได้ศึกษามา
วิธีทำ ก. จากสมการความเร็วเป็นฟังก์ชั่นของตำแหน่ง
![]() =
= ![]()
วัตถุจะมีความเร็วสูงสุดเมื่ออยู่ที่จุดสมดุล
![]()
![]() =
= ![]()
![]() =
= ![]()
ข. จากสมการความเร่งเป็นฟังก์ชั่นของตำแหน่ง ความเร่งจะมีค่ามากสุด
เมื่อ ![]() มีค่ามากสุด
มีค่ามากสุด
![]()
![]() =
= ![]()
![]() =
= ![]()
นอกจากนี้ผลลัพธ์ที่ได้ยังสามารถคำนวณได้จากสมการความเร็วเป็นฟังก์ชั่นของเวลา และความเร่งเป็นฟังก์ชั่นของเวลา
ค. คาบการแกว่ง สามารถหาได้จากสมการตำแหน่งเป็นฟังก์ชั่นของเวลา เมื่อวัตถุเคลื่อนที่ครบหนึ่งรอบแล้ววัตถุจะกลับมายังตำแหน่งเดิมจาก
![]() =
= ![]()
= ![]()
นั่นคือ
![]() =
= ![]()
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เหมือนการเคลื่อนที่แบบวงกลม
15.3 ความสัมพันธ์กับการเคลื่อนที่แบบวงกลม
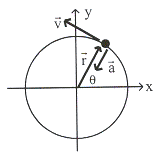 เมื่อวัตถุเคลื่อนที่เป็นวงกลมดังรูปที่
15.4 ความเร็วเชิงมุมคือ
เมื่อวัตถุเคลื่อนที่เป็นวงกลมดังรูปที่
15.4 ความเร็วเชิงมุมคือ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
ความสัมพันธ์ระหว่างความเร็วเชิงเส้นและความเร็วเชิงมุมคือ
![]() =
= ![]()
ความสัมพันธ์ระหว่างความเร่งสู่ศูนย์กลางและความเร็วเชิงมุมคือ
![]() =
=
![]() =
=
![]()
รูปที่ 15.4 ![]() =
= ![]()
ตำแหน่ง ความเร็ว และความเร่งของวัตถุเมื่อเขียนอยู่ในรูปฟังก์ชั่นของเวลา
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
จะสังเกตได้ว่าสมการที่ได้คล้ายกับสมการการเคลื่อนที่ของมวลติดปลายสปริง
เมื่อ ![]() หรือ
หรือ
![]() เป็นองค์ประกอบของการเคลื่อนที่แบบวงกลม
ซึ่งก็คือการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
เป็นองค์ประกอบของการเคลื่อนที่แบบวงกลม
ซึ่งก็คือการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
15.4 แรงและพลังงานในการเคลื่อนที่แบบซิมเปิลฮาร์โมนิกอย่างง่าย
เมื่อมวล
![]() ถูกกระทำด้วยแรง
ถูกกระทำด้วยแรง
![]() ทำให้เคลื่อนที่ด้วยความเร่ง
ทำให้เคลื่อนที่ด้วยความเร่ง
![]() จากกฎการเคลื่อนที่ข้อสองของนิวตัน
จากกฎการเคลื่อนที่ข้อสองของนิวตัน
![]() =
= ![]()
เนื่องจากวัตถุเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
![]()
![]() =
= ![]() =
= ![]()
= ![]()
พิจารณาพลังงานศักย์ของสปริง จาก
![]() =
= ![]()
![]() =
= ![]()
อินทิเกรตโดยให้พลังงานศักย์เป็นศูนย์ ที่จุดสมดุล
![]() =
= ![]()
![]() =
= ![]()
แต่ความถี่เชิงมุมของวัตถุที่ติดปลายสปริงคือ
![]()
![]()
![]() =
= ![]()
นั่นคือพลังงานศักย์จะเป็นศูนย์ที่
![]() และมีค่ามากที่สุดที่
และมีค่ามากที่สุดที่
![]()
พลังงานจลน์ของวัตถุจาก
![]() =
= ![]()
เนื่องจากวัตถุเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
![]()
![]() =
= ![]()
= ![]()
![]() =
= ![]()
จะเห็นว่าพลังงานจลน์จะมีค่ามากที่สุดที่จุดสมดุล
![]() และเป็นศูนย์ที่
และเป็นศูนย์ที่
![]()
ดังนั่นจะได้พลังงานรวมทั้งหมดของการเคลื่อนที่แบบซิมเปิลฮาร์โมนิกอย่างง่ายคือ
![]() =
= ![]()
= ![]() +
+ ![]()
= ![]() =
= ![]()
ตัวอย่างที่
15.5
สปิงมีค่าคงตัวของสปริง ![]() วางอยู่ในแนวระดับบนโต๊ะซึ่งไม่มีแรงเสียดทาน
ที่ปลายสปริงติดวัตถุมวล
วางอยู่ในแนวระดับบนโต๊ะซึ่งไม่มีแรงเสียดทาน
ที่ปลายสปริงติดวัตถุมวล ![]() เมื่อดึงวัตถุให้ยืดออก
เมื่อดึงวัตถุให้ยืดออก ![]() จากตำแหน่งสมดุลแล้วปล่อยวัตถุจะเคลื่อนที่แแลซิมเปิลฮาร์โมนิก
จงหา
จากตำแหน่งสมดุลแล้วปล่อยวัตถุจะเคลื่อนที่แแลซิมเปิลฮาร์โมนิก
จงหา
ก. แรงที่สปริงกระทำต่อวัตถุก่อนปล่อย
ข. คาบภายหลังจากที่ปล่อยวัตถุ
ค. แอมปลิจูดของการเคลื่อนที่
จ. ความเร่งสูงสุดของวัตถุ
ฉ. ความเร็ว ความเร่ง พลังงานจลน์ และ พลังงานศักย์ เมื่อวัตถุเคลื่อนที่ได้ครึ่งทางจากตำแหน่งเริ่มต้นเข้าหาตำแหน่งสมดุล
ช. พลังงานรวมทั้งหมดของการเคลื่อนที่
ซ. การกระจัดของวัตถุเป็นฟังก์ชั่นของเวลา
วิธีทำ ก. หาแรงที่สปริงกระทำต่อวัตถุก่อนปล่อย
![]() =
= ![]() =
= ![]()
= ![]()
ข. หาคาบภายหลังจากที่ปล่อยวัตถุ
![]() =
= ![]() =
= ![]()
= ![]()
ค. หาแอมปลิจูดของการเคลื่อนที่
แอมปลิจูดการกระจัดมากที่สุด
![]()
ง. หาความเร็วสูงสุดของวัตถุ
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
= ![]()
ความเร็วสูงสุดจะอยู่ที่จุดสมดุล ![]() คือจุดที่พลังงานจลน์สูงสุด
จะมีสองค่า
คือจุดที่พลังงานจลน์สูงสุด
จะมีสองค่า ![]() คือขณะที่ผ่านจุดสมดุลขณะไปและกลับ
คือขณะที่ผ่านจุดสมดุลขณะไปและกลับ
จ. หาความเร่งสูงสุดของวัตถุ
![]() =
= ![]()
= ![]()
= 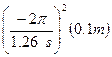
= ![]()
ความเร่งจะมีค่าสูงสุดที่ปลายสุดของเส้นทาง ![]() นั่นคือความเร่งจะมีสองค่า
นั่นคือความเร่งจะมีสองค่า ![]() คือขณะที่แอมปลิจูลเท่ากับ
คือขณะที่แอมปลิจูลเท่ากับ
![]() และ
และ ![]()
ฉ. หาความเร็ว ความเร่ง พลังงานจลน์ และ พลังงานศักย์ เมื่อวัตถุเคลื่อนที่ได้ครึ่งทางจากตำแหน่ง เริ่มต้นเข้าหาตำแหน่งสมดุล
เมื่อ ![]() =
= ![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
![]() =
= ![]() =
= ![]()
= 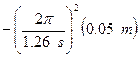
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ช. หาพลังงานรวมทั้งหมดของการเคลื่อนที่
![]() =
= ![]()
= ![]() =
= ![]()
หรือ ![]() =
= ![]() =
= ![]()
= ![]()
ซ.หาการกระจัดของวัตถุเป็นฟังก์ชั่นของเวลา
จาก ![]() =
= ![]()
เมื่อ
![]() ;
; ![]() ; และที่
; และที่
![]() ;
;
![]() จะได้
จะได้
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
จะได้
![]() =
= ![]() หรือ
หรือ
= ![]()
15.5 รูปแบบต่าง ๆ ของการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
ก. ลูกตุ้มนาฬิกาอย่างง่าย (Simple Pendulum)
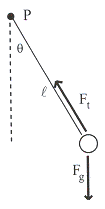
พิจารณาวัตถุที่ปลายเชือกเบาดังรูปที่ 15.5 แรงที่กระทำต่อวัตถุประกอบด้วย
แรงโน้มถ่วง ![]() กับแรงตึงเชือก
กับแรงตึงเชือก
![]() ให้
ให้ ![]() เป็นจุดหมุน
แรงตึงเชือกจะไม่ทำให้เกิดทอร์ก แรงที่มีผลต่อการหมุนคือแรงโน้มถ่วง
จากสมการการหมุน
เป็นจุดหมุน
แรงตึงเชือกจะไม่ทำให้เกิดทอร์ก แรงที่มีผลต่อการหมุนคือแรงโน้มถ่วง
จากสมการการหมุน
![]() =
= ![]()
![]() =
= ![]()
(ให้ ![]() คือความยาวเชือก)
คือความยาวเชือก)
![]() =
= ![]()
![]() =
= ![]()
เมื่อแกว่งเป็นมุมเล็ก
ๆ จะได้ว่า
![]()
![]()
![]()
![]()
![]()
![]()
สมการที่ได้คือสมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก ความเร่ง
เชิงมุมจะเป็นปฎิภาคโดยตรงกับการกระจัดเชิงมุม ![]() แต่ทิศตรงกันข้าม
แต่ทิศตรงกันข้าม
รูปที่
15.5 เปรียบเทียบกับสมการการเคลื่อนที่ของมวลที่ติดปลายสปริง
เมื่อเปรียบเทียบความเร่ง ![]() การกระจัด
การกระจัด ![]()
ดังนั้นสมการการเคลื่อนที่เชิงมุม
![]() จะเป็นการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
จะได้ความถี่เชิงมุมของการแกว่งแบบลูกตุ้มนาฬิกาอย่างง่าย
จะเป็นการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
จะได้ความถี่เชิงมุมของการแกว่งแบบลูกตุ้มนาฬิกาอย่างง่าย
![]() =
= ![]()
ตัวอย่างที่
15.6
จงหาความยาวเชือกของการแก่วงแบบลูกตุ้มนาฬิกาอย่างง่าย ที่ทำให้คาบการแก่วงมีค่า ![]()
วิธีทำ ![]() =
= ![]()
แต่ ![]() =
= ![]() =
= ![]()
![]() =
= ![]() =
= ![]()
![]() =
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
ข. ลูกตุ้มทอร์ชั่น (Torsional Pendulum)
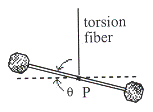
จากรูปที่ 15.6 เมื่อบิดมวลซึ่งติดอยู่ที่ปลายแท่งโลหะเบาเป็นมุมน้อย ๆ ![]() โดยที่จุดกึ่งกลางของแท่งโลหะตรึงติดกับปลายลวดแล้วปล่อย
เส้นลวดจะทำให้เกิดทอร์คบนระบบมวลทั้งสองเกิดการบิดไปมารอบจุด
โดยที่จุดกึ่งกลางของแท่งโลหะตรึงติดกับปลายลวดแล้วปล่อย
เส้นลวดจะทำให้เกิดทอร์คบนระบบมวลทั้งสองเกิดการบิดไปมารอบจุด ![]() จะได้
จะได้
![]() =
= ![]()
เมื่อ ![]() เรียกว่าค่าคงที่ของการบิด
(torsion constant)
เรียกว่าค่าคงที่ของการบิด
(torsion constant)
จากสมการการหมุน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 15.6
สมการที่ได้คือสมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก ความเร่งเชิงมุมจะแปรผันตรงกับการกระจัดเชิงมุมโดยมีทิศทางตรงกันข้าม จะได้ความถี่เชิงมุมของการแกว่งแบบลูกตุ้มทอร์ชั่นคือ
![]() =
= ![]()
![]() คือโมเมนต์ความเฉื่อยของมวลทั้งสองที่ติดอยู่ที่ปลายแท่งโลหะเบา
คือโมเมนต์ความเฉื่อยของมวลทั้งสองที่ติดอยู่ที่ปลายแท่งโลหะเบา
ตัวอย่างที่
15.7
จากรูปที่ 15.6 ถ้ามวลทั้งสองอยู่ห่างกัน ![]() มวลแต่ละก้อนมีค่า
มวลแต่ละก้อนมีค่า ![]() ถ้าคาบการแกว่งมีค่า
ถ้าคาบการแกว่งมีค่า
![]() จงหาค่าคงที่ของการแกว่ง
จงหาค่าคงที่ของการแกว่ง
วิธีทำ จากความถี่เชิงมุมของการแกว่งแบบลูกตุ้มทอร์ชั่น
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อโมเมนต์ความเฉื่อยของมวลที่ติดอยู่ที่ปลายแท่งโลหะเบาและมีจุดหมุนอยู่ที่จุดหมุนอยู่ที่จุดกึ่งกลางของแท่งโลหะเบา
![]() =
= ![]()
= ![]()
![]() =
= 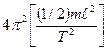
= ![]()
= 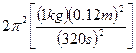
= ![]()
ค.ลูกตุ้มฟิสิกัล (Physics Pendulum)
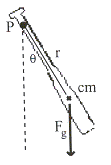 ลูกตุ้มฟิสิกัลป์ประกอบด้วยวัตถุเนื้อเดียวกัน
โดยมีแรงโน้มถ่วงที่กระทำผ่านจุดศูนย์กลางมวล
ลูกตุ้มฟิสิกัลป์ประกอบด้วยวัตถุเนื้อเดียวกัน
โดยมีแรงโน้มถ่วงที่กระทำผ่านจุดศูนย์กลางมวล ![]() ทำให้เกิดทอร์ก จากรูปที่ 15.7
ไม้เบสบอลแขวนอยู่ที่ปลายด้านหนึ่ง แรงโน้มถ่วงจะทำให้เกิดการหมุนรอบจุด
ทำให้เกิดทอร์ก จากรูปที่ 15.7
ไม้เบสบอลแขวนอยู่ที่ปลายด้านหนึ่ง แรงโน้มถ่วงจะทำให้เกิดการหมุนรอบจุด ![]() จากสมการการหมุน
จากสมการการหมุน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 15.7
เมื่อ ![]() และ
และ
![]() จะขึ้นอยู่กับตำแหน่งของจุดหมุน
ถ้าให้
จะขึ้นอยู่กับตำแหน่งของจุดหมุน
ถ้าให้ ![]() แกว่งเป็นมุมน้อย
ๆ จะได้
แกว่งเป็นมุมน้อย
ๆ จะได้ ![]() จะได้
จะได้
![]() =
= ![]()
สมการที่ได้คือสมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิกอย่างง่าย ความเร่งเชิงมุมจะแปรผันตรงกับการกระจัดเชิงมุมแต่มีทิศตรงกันข้าม จะได้ความถี่เชิงมุมของการแกว่งของลูกตุ้มนาฬิกาอย่างง่ายคือ
![]() =
= ![]()
ตัวอย่างที่ 15.8 จากรูปที่ 15.7 จงหาโมเมนต์ความเฉื่อยของไม้เบสบอล
วิธีทำ จากสมการความถี่เชิงมุมของการแกว่งของลูกตุ้มนาฬิกาอย่างง่าย
![]() =
= ![]()
![]() =
= ![]()
กำหนดให้
โมเมนต์ความเฉื่อยของไม้เบสบอลรอบจุด
![]() มีค่า
มีค่า ![]() เมื่อ
เมื่อ ![]() เป็นค่าคงที่ ;
เป็นค่าคงที่ ;![]() เป็นมวลของ ไม้เบสบอล
;
เป็นมวลของ ไม้เบสบอล
; ![]() คือความยาวของไม้เบสบอล ;
คือความยาวของไม้เบสบอล ; ![]() คือระยะห่างจากจุดหมุนถึงจุดศูนย์กลางมวล
;
คือระยะห่างจากจุดหมุนถึงจุดศูนย์กลางมวล
; ![]() คือคาบการแกว่ง
คือคาบการแกว่ง
![]() =
= ![]()
จาก
![]() =
= ![]()
จะได้
![]() =
= ![]()
ให้ ![]() ;
;
![]() ;
; ![]() และ
และ
![]()
![]() =
= ![]()
= ![]()
![]() =
= ![]()
นั่นคือค่าโมเมนต์ความเฉื่อยของไม้เบสบอลเมื่อจุดหมุนอยู่ที่ปลาย จะมีค่ามากกว่า 1 ใน 3 ของโมเมนต์ความเฉื่อยของวัตถุรูปร่างสม่ำเสมอและมีจุดหมุนอยู่ที่ปลาย
ตัวอย่างที่
15.9
ไม้คอร์ดรูปสี่เหลี่ยมจัตุรัสที่มีความยาวด้าน ![]() มีความหนาแน่น
มีความหนาแน่น ![]() ลอยอยู่ในน้ำ
จากนั้นกดให้ไม้คอร์ดจมลงไปมากกว่าระดับสมดุลดังรูปที่ 15.8 แล้วปล่อยให้ไม้คอร์ดเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
จงหาคาบของการสั่น
ลอยอยู่ในน้ำ
จากนั้นกดให้ไม้คอร์ดจมลงไปมากกว่าระดับสมดุลดังรูปที่ 15.8 แล้วปล่อยให้ไม้คอร์ดเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
จงหาคาบของการสั่น
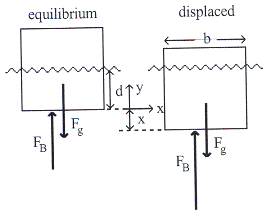 วิธีทำ
จากกฎการเคลื่อนที่ข้อสองของนิวตันเมื่อระบบสมดุล
วิธีทำ
จากกฎการเคลื่อนที่ข้อสองของนิวตันเมื่อระบบสมดุล
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
จากกฎของอาร์คิมิดีส
![]() =
= ![]()
![]() =
= ![]()
เมื่อ
![]() คือความหนาแน่นของน้ำ ;
คือความหนาแน่นของน้ำ ; ![]() คือความหนาแน่นของไม้คอร์ด
;
คือความหนาแน่นของไม้คอร์ด
; ![]() คือปริมาตรส่วนที่จม ;
คือปริมาตรส่วนที่จม ; ![]() คือปริมาตรทั่งหมด
คือปริมาตรทั่งหมด
รูปที่ 15.8
จากฎข้อสองของนิวตัน และจากกฎของอาร์คิมิดีส เมื่อไม้คอร์ดมีการเคลื่อนที่
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แต่ ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
จะได้ความเร่งของไม้คอร์ดคือ
![]() =
= ![]()
นั่นคือความเร่งจะแปรผันตรงกับระยะที่จมแต่มีทิศตรงกันข้าม สมการที่ได้คือสมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิกอย่างง่าย โดยมีความถี่เชิงมุมคือ
![]() =
= ![]()
![]() =
= 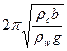
= 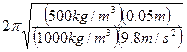
= ![]()
สรุป
กฎของฮุค
: ![]()
สมการการเคลื่อนที่แบบซิมเปิลฮาร์โมนิก
![]()
![]()
![]()
![]()
![]()
ความถี่เชิงมุม
Spring ![]()
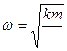
Simple
pendulum ![]()
![]()
Torsional
pendulum ![]()
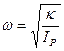
Physics
pendulum ![]()