Recipe 1.14 Finding the Length of Any Three Sidesof a Right Triangle

Problem

You need to calculate the length of one side of a triangle when either the lengths of two sides are known or one angle and the length of a side are known.

Solution

Use the Math.Sin, Math.Cos, and Math.Tan methods of the Math class to find the length of one side. The equations for these methods are as follows:

double theta = 40;
double hypotenuse = 5;
double oppositeSide;
double adjacentSide;

oppositeSide = Math.Sin(theta) * hypotenuse;
oppositeSide = Math.Tan(theta) * adjacentSide;
adjacentSide = Math.Cos(theta) * hypotenuse;
adjacentSide = oppositeSide / Math.Tan(theta);
hypotenuse   = oppositeSide / Math.Sin(theta);
hypotenuse   = adjacentSide / Math.Cos(theta);

where theta (Q) is the known angle, and the oppositeSide variable is equal to the length of the side opposite to the angle theta, and the adjacentSide variable is equal to the length of the side adjacent to the angle theta. The hypotenuse variable is equal to the length of the hypotenuse of the triangle. See Figure 1-1.

Figure 1-1. A right triangle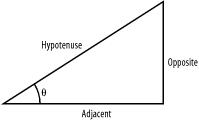

In addition to these three static methods, the length of the hypotenuse of a right triangle can be calculated using the Pythagorean theorem. This theorem states that the hypotenuse of a right triangle is equal to the square root of the sum of the squares of the other two sides. This equation can be realized through the use of the Math.Pow and Math.Sqrt static methods of the Math class, as follows:

double hypotenuse = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2))

where xSide and ySide are the lengths of the two sides that are not the hypotenuse of the triangle.

Discussion

Finding the length of a side of a right triangle is easy when an angle and the length of one of the sides are known. Using the trigonometric functions sine, cosine, and tangent, we can derive the lengths of either of the two unknown sides. The equations for sine, cosine, and tangent are defined here:

sin(Theta) = oppositeSide / hypotenuseSide
cos(Theta) = adjacentSide / hypotenuseSide
tan(Theta) = oppositeSide / adjacentSide

where theta is the value of the known angle. Rearranging these equations allows us to derive the following equations:

oppositeSide = sin(theta) * hypotenuse;
oppositeSide = tan(theta) * adjacentSide;
adjacentSide = cos(theta) * hypotenuse;
adjacentSide = oppositeSide / tan(theta);
hypotenuse   = oppositeSide / sin(theta);
hypotenuse   = adjacentSide / cos(theta);

These equations give us two methods to find the length of each side of the triangle.

In the case where none of the angles are known, but the lengths of two of the sides are known, use the Pythagorean theorem to determine the length of the hypotenuse. This theorem is defined as follows:

Math.Sqrt(Math.Pow(hypotenuse)) = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2))

Simplifying this equation into a syntax usable by C#, we obtain the following code:

double hypotenuse = Math.Sqrt(Math.Pow(xSide, 2) + Math.Pow(ySide, 2));

where hypotenuse is equal to the length of the hypotenuse, and xSide and ySide are the lengths of the other two sides.

See Also

See the "Math Class" topic in the MSDN documentation.