|
|
|
13.50 <valarray>The <valarray> header declares types and functions for operating on arrays of numerical values. The intention is to provide types that could be optimized on certain hardware platforms for computationally-intensive programs. The consensus in the C++ user community seems to be that the standard failed to live up to the intentions. Several other numerical libraries, such as Blitz++ and MTL, provide high-performance matrix solutions. (See Appendix B for more information about Blitz++.) Most programs do not need <valarray>. A valarray is a class template that represents a one-dimensional array of numerical values. The array can grow at runtime. All the arithmetic operators and mathematical functions are overloaded to work with two valarray arguments or with a valarray and a scalar. You can also work with parts of an array: slices, generalized slices, masks, and indirect arrays. A slice is a set of elements of a valarray, with a starting index, a count, and a stride (an index interval). A generalized slice (gslice) lets the stride count and length vary, which can be used to implement multidimensional arrays. A mask is a valarray of flags, in which the flags indicate whether the corresponding item is part of the masked array. An indirect array is an array of indices. Each of these concepts is explained in this section. The most important distinguishing feature of valarrays is that they do not allow aliasing, that is, an object cannot be an element of more than one valarray. This enables additional optimizations that are not possible on ordinary arrays. Because valarray is optimized for performance, no error-checking is performed. Referring to an index out of range or operating on arrays of different size result in undefined behavior—the same as with ordinary arrays. Unlike ordinary arrays, a convenient size( ) member function helps to ensure that you do not make mistakes. See the <cmath> header for scalar mathematical functions and <numeric> for a few numeric algorithms. See <complex> for complex numbers. Throughout this section, examples show valarray objects and subsets printed using operator<<, which is shown in Example 13-40. Example 13-40. Printing a valarray or subset array// Print a valarray on one line, enclosed by curly braces. For example:
// "{ 1 2 3 }".
template<typename T>
void print_valarray(std::ostream& out, const std::valarray<T>& a)
{
out << '{';
for (size_t i = 0; i < a.size( ); ++i)
out << ' ' << a[i];
out << " }";
}
// Print a slice_array, gslice_array, etc. by converting to a valarray.
// Converting a valarray to a valarray is wasteful, but harmless for these simple
// examples.
template<template<typename T> class U, typename T>
std::ostream& operator<<(std::ostream& out, const U<T>& x)
{
print_valarray(out, static_cast<std::valarray<T> >(x));
return out;
}
The abs function computes the absolute value of each element of a. See Alsoabs in <cmath>, abs in <cstdlib>
The acos function computes the inverse cosine of each element of a. See Alsoacos in <cmath>
The asin function computes the inverse sine of each element of a. See Alsoasin in <cmath>
The atan function computes the inverse tangent of each element of a. See Alsoatan2 function template, atan in <cmath>
The atan2 function computes the inverse tangent of y/x, in which y is a scalar or an element of b, and x is a scalar or an element of a. See Alsoatan function template, atan2 in <cmath>
The cos function computes the cosine of each element of a. See Alsocos in <cmath>
The cosh function computes the hyperbolic cosine of each element of a. See Alsocosh in <cmath>
The exp function computes the exponential ex for each element x of a. See Alsoexp in <cmath>
The gslice class describes a generalized slice of a valarray. A generalized slice is a subset of the elements of a valarray, characterized by a starting index and a set of sizes and strides. The size and stride arrays must have the same size. Each size/stride pair denotes a set of elements at periodic indices. The number of elements in the generalized slice is equal to the product of the values in the size array. The elements are taken from a valarray at each index i:
in which kj takes all the values in the range [0, size[j]), and j is in the range [0, stride.size( )). The highest value of j varies fastest. With a single element in stride and size, gslice is the same as plain slice. Example 13-41 demonstrates gslice more clearly. Pay particular attention to the final gslice, where you can see how the indices advance, first with a stride of 3 (k1 ranges from 0 to 2), then with a stride of 2 (k0 ranges from 0 to 3) ExampleExample 13-41. Generalized slicing of a valarray// Construct valarray objects from a few integers.
std::valarray<std::size_t> va(std::size_t a0)
{
std::valarray<std::size_t> result(1);
result[0] = a0;
return result;
}
std::valarray<std::size_t> va(std::size_t a0, std::size_t a1)
{
std::valarray<std::size_t> result(2);
result[0] = a0;
result[1] = a1;
return result;
}
int main( )
{
using namespace std;
valarray<int> a(24);
for (size_t i = 0; i < a.size( ); ++i)
a[i] = i;
cout << a << '\n';
// Prints { 0 1 2 3 4 5 6 7 8 9 10 11 ... 20 21 22 23 }
cout << a[slice(1, 4, 3)] << '\n';
// Prints { 1 4 7 10 }
cout << a[gslice(1, va(4), va(3))] << '\n';
// Prints { 1 4 7 10 }
const valarray<int> const_a(a);
cout << const_a[gslice(2, va(4, 3), va(2, 3))] << '\n';
// Prints { 2 5 8 4 7 10 6 9 12 8 11 14 }
}
Notice also that the final gslice requires a const valarray. This is because it contains degenerate slices, in which an element (e.g., 8) appears more than once in the result. The aliasing rules of a valarray prohibit multiple references to the same element, so if a const valarray were not used, the results would be undefined. By using a const valarray, the result is a copy of the sliced elements, so the two occurrences of element 8 are separate objects, not aliases for the same object, and disaster is averted. A generalized slice is most often used to represent a multidimensional array. For example, you can treat a valarray of 24 elements as a 2 x 3 x 4 matrix. To extract a plane of the matrix, you can use a gslice. Figure 13-27 depicts the matrix and the plane. Example 13-42 shows the code. Figure 13-27. A 3-D matrix stored in a valarray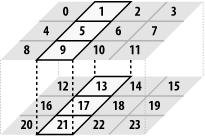 Example 13-42. Using gslice for multidimensional arrays// See Example 13-41 for the va function. int main( ) { using namespace std; valarray<int> a(24); for (size_t i = 0; i < a.size( ); ++i) a[i] = i; cout << a[gslice(1, va(2, 3), va(12, 4))] << '\n'; // Prints: { 1 5 9 13 17 21 } } To create an n-dimensional submatrix of an m-dimensional matrix, the size and stride arrays must both have length n. The size array determines the dimensions of the result. Use the subscript operator to take a generalized slice of a valarray. You can assign a valarray to a generalized slice, in which the righthand side of the assignment must have the same size as the size of the slice. You can also convert the slice to a valarray, which copies only those elements of the slice to the new valarray. When you take a generalized slice of a valarray, the result is a gslice_array object, but the gslice_array type is mostly transparent to the programmer. See gslice_array later in this section for details. See Alsogslice_array class template, slice class
The gslice_array class template represents a subset of the elements of a valarray, called a generalized slice. To create a generalized slice, use valarray's operator[] with an argument of type gslice. For some operations, the gslice_array object is transparent. In particular, you can assign a valarray to a gslice_array object (provided they have the same size), or you can construct a new valarray from a gslice_array. If you want to perform other operations, such as non-assignment arithmetic, you must explicitly convert the gslice_array to valarray, as demonstrated in Example 13-43. ExampleExample 13-43. Using gslice_array// See Example 13-41 for the va function. int main( ) { using namespace std; const int data[] = { 1, 2, 3, 4, 5, 6, 7, 8 }; valarray<int> a(data, sizeof(data)/sizeof(data[0])); cout << a << '\n'; // Prints { 1 2 3 4 5 6 7 8 } cout << a[gslice(1, va(2, 2), va(4, 2))] << '\n' << a[gslice(0, va(2, 2), va(4, 2))] << '\n'; // prints: // { 2 4 6 8 } // { 1 3 5 7 } // operator+ is not defined for gslice_array, so cast to valarray to perform // addition. cout << static_cast<valarray<int> >(a[gslice(1, va(2,2), va(4,2))]) + static_cast<valarray<int> >(a[gslice(0, va(2,2), va(4,2))]) << '\n'; // Prints: { 3 7 11 15 } // Simple assignment does not require casting. a[gslice(0, va(2, 2), va(4, 2))] = 0; cout << a << '\n'; // Prints: { 0 2 0 4 0 6 0 8 } // Computational assignment does not require casting. valarray<int> ten(10, 4); a[gslice(1, va(2, 2), va(4, 2))] *= ten; cout << a << '\n'; // Prints: { 0 20 0 40 0 60 0 80 } } The members of gslice_array are straightforward. When using any of the assignment operators, the valarray on the righthand side must be the same size as the gslice_array on the lefthand side. You can also assign a scalar to every element of the array. Note that the default constructor, copy constructor, and copy assignment operator are all private. The purpose of this is to restrict the use of gslice_array so it can be used only as a return value from valarray's operator[]. See Alsogslice class, indirect_array class template, mask_array class template, slice_array class template, valarray class template
The indirect_array class template represents a subset of the elements of a valarray. To create an indirect subset, use valarray's operator[] with an argument of type valarray<size_t>. The elements of the argument are the desired indices in the subset. For some operations, the indirect_array object is transparent. In particular, you can assign a valarray to an indirect_array object (provided they have the same size), or you can construct a new valarray from an indirect_array. If you want to perform other operations, such as non-assignment arithmetic, you must explicitly convert the indirect_array to valarray, as demonstrated in Example 13-44. ExampleExample 13-44. Using indirect_arrayint main( )
{
using namespace std;
const int data[] = { 1, 2, 3, 4, 5, 6, 7, 8 };
valarray<int> a(data, sizeof(data)/sizeof(data[0]));
cout << a << '\n';
// Prints: { 1 2 3 4 5 6 7 8 }
// Specify the indices into a.
const size_t p[] = { 2, 3, 5, 7 };
valarray<size_t> indices(p, sizeof(p)/sizeof(p[0]));
cout << a[indices] << '\n';
// Prints: { 3 4 6 8 }
// Add 10 to the elements at the desired indices.
valarray<int> ten(10, 4);
a[indices] += ten;
cout << a << '\n';
// Prints: { 1 2 13 14 5 16 7 18 }
// Must cast to perform ordinary arithmetic.
cout << static_cast<valarray<int> >(a[indices])
* ten << '\n';
// Prints: { 130 140 160 180 }
}
The members of indirect_array are straightforward. When using any of the assignment operators, the valarray on the righthand side must be the same size as the indirect_array on the lefthand side. You can also assign a scalar to every element of the array. Note that the default constructor, copy constructor, and copy assignment operator are all private. The purpose of this is to restrict the use of indirect_array so it can be used only as a return value from valarray's operator[]. See Alsogslice_array class template, mask_array class template, slice_array class template, valarray class template
The log function computes the natural (base e) logarithm of each element of a. See Alsolog in <cmath>
The log10 function computes the common (base 10) logarithm of each element of a. See Alsolog10 in <cmath>
The mask_array class template represents a subset of the elements of a valarray. To create a mask subset, use valarray's operator[] with an argument of type valarray<bool>. An element is included in the result set if the corresponding element in the argument is true. For some operations, the mask_array object is transparent. In particular, you can assign a valarray to a mask_array object (provided they have the same size), or you can construct a new valarray from a mask_array. If you want to perform other operations, such as non-assignment arithmetic, you must explicitly convert the mask_array to valarray, as demonstrated in Example 13-45. ExampleExample 13-45. Using mask_array// Simple average
template<typename T>
T avg(const std::valarray<T>& a)
{
return a.sum( ) / a.size( );
}
int main( )
{
using namespace std;
const int data[] = { 1, -3, 10, 42, -12, 13, -7, 69 };
valarray<int> a(data, sizeof(data)/sizeof(data[0]));
cout << a << '\n';
// Prints: { 1 -3 10 42 -12 13 -7 69 }
// Print the values that are above average.
cout << "avg=" << avg(a) << '\n';
cout << a[a > avg(a)] << '\n';
// Prints: { 42 69 }
// Force all negative values to be 0. Notice how no cast is needed for the
// simple assignment.
a[a < 0] = 0;
cout << a << '\n';
// Prints: { 1 0 10 42 0 13 0 69 }
// Other operations, such as multiplication by a scalar, are defined only for
// valarray, so a cast is needed.
cout << static_cast<valarray<int> >(a[a > 0]) * -1 << '\n';
// Prints: { -1 -10 -42 -13 -69 }
}
The members of mask_array are straightforward. When using any of the assignment operators, the valarray on the righthand side must be the same size as the mask_array on the lefthand side. You can also assign a scalar to every element of the array. Note that the default constructor, copy constructor, and copy assignment operator are all private. The purpose of this is to restrict the use of mask_array so it can be used only as a return value from valarray's operator[]. See Alsogslice_array class template, indirect_array class template, slice_array class template, valarray class template
The * operator performs elementwise multiplication. It multiplies each x * y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When multiplying two arrays, they must have the same size. The resulting array has the same size as the argument array(s).
The / operator performs elementwise division. It divides each x / y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When dividing two arrays, they must have the same size. The resulting array has the same size as the argument array(s).
The + operator performs elementwise addition. It adds each x + y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When adding two arrays, they must have the same size. The resulting array has the same size as the argument array(s).
The - operator performs elementwise subtraction. It subtracts each x - y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When subtracting two arrays, they must have the same size. The resulting array has the same size as the argument array(s).
The & operator performs bitwise and on each x & y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator & is defined.
The | operator performs bitwise inclusive or on each x | y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator | is defined.
The ^ operator performs bitwise exclusive or on each x ^ y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator ^ is defined.
The >> operator performs right shift on each x >> y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator >> is defined.
The << operator performs left shift on each x << y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator << is defined.
The && operator performs logical and on each x && y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator && is defined. As with any other overloaded operator &&, short-cut evaluation is not supported.
The || operator performs logical or on each x || y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator || is defined and yields a bool result or a result that can be converted to bool. As with any other overloaded operator ||, short-cut evaluation is not supported.
The == operator compares each x == y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator == is defined and yields a bool result or a result that can be converted to bool.
The != operator compares each x != y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator != is defined and yields a bool result or a result that can be converted to bool.
The < operator compares each x < y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator < is defined and yields a bool result or a result that can be converted to bool.
The <= operator compares each x <= y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator <= is defined and yields a bool result or a result that can be converted to bool.
The > operator compares each x > y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator > is defined and yields a bool result or a result that can be converted to bool.
The >= operator compares each x >= y, in which x is a scalar or an element of a, and y is a scalar or an element of b. When operating on two arrays, they must have the same size. The resulting array has the same size as the argument array(s). The type T must be one for which operator >= is defined and yields a bool result or a result that can be converted to bool.
The pow function computes the power xy, in which x is a scalar or an element of a, and y is a scalar or an element of b. See Alsopow in <cmath>
The sin function computes the sine of the elements of a. See Alsosin in <cmath>
The sinh function computes the hyperbolic sine of the elements of a. See Alsosinh in <cmath>
The slice class describes a slice of a valarray. A slice is a subset of the elements of a valarray at periodic indices. The slice has a starting index, a size, and a stride, in which the stride is the index interval. Figure 13-28 depicts slice(1,3,4) of a valarray. Figure 13-28. Slicing a valarray Use the subscript operator to take a slice of a valarray. You can assign a valarray to a slice, in which the righthand side of the assignment must have the same size as the size of the slice. You can also convert the slice to a valarray, which copies only those elements of the slice to the new valarray. When you take a slice of a valarray, the result is a slice_array object, but the slice_array type is mostly transparent to the programmer. See slice_array later in this section for details. You can use a slice to treat a valarray as a two-dimensional matrix. A slice can specify a row or column of the matrix. For an n x m matrix, row r is slice(r*m, m, 1), and column c is slice(c, n, m), as you can see in Example 13-46. ExampleExample 13-46. A simple 2-D matrix classtemplate<typename T>
class matrix2D {
public:
matrix2D(std::size_t rows, std::size_t columns) :
rows_(rows), cols_(columns), data_(rows * columns) {}
std::size_t rows( ) const { return rows_; }
std::size_t cols( ) const { return cols_; }
std::valarray<T> row(std::size_t r) const
{ return data_[std::slice(r*cols( ),cols( ), 1)]; }
std::valarray<T> col(std::size_t c) const
{ return data_[std::slice(c, rows( ), cols( ))]; }
std::slice_array<T> row(std::size_t r)
{ return data_[std::slice(r*cols( ),cols( ), 1)]; }
std::slice_array<T> col(std::size_t c)
{ return data_[std::slice(c, rows( ), cols( ))]; }
T& operator( )(std::size_t r, std::size_t c)
{ return data_[r*cols( )+c]; }
T operator( )(std::size_t r, std::size_t c) const
{ return row(r)[c]; }
matrix2D<T> transpose( ) {
matrix2D<T> result(cols( ), rows( ));
for (std::size_t i = 0; i < rows( ); ++i)
result.col(i) = static_cast<std::valarray<T> >(row(i));
return result;
}
private:
std::size_t rows_;
std::size_t cols_;
std::valarray<T> data_;
};
See Alsogslice class, slice_array class template
The slice_array class template represents a subset of the elements of a valarray, taken at periodic indices, called a slice. To create a slice, use valarray's operator[] with an argument of type slice. For some operations, the slice_array object is transparent. In particular, you can assign a valarray to a slice_array object (provided they have the same size), or you can construct a new valarray from a slice_array. If you want to perform other operations, such as non-assignment arithmetic, you must explicitly convert the slice_array to valarray, as demonstrated in Example 13-47. ExampleExample 13-47. Slicing a valarrayint main( )
{
using namespace std;
const int data[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13 };
valarray<int> v(data, sizeof(data)/sizeof(data[0]));
const int newdata[] = { 30, 70, 110 };
valarray<int> rpl(newdata, 3);
v[slice(2, 3, 4)] = rpl;
cout << v << '\n';
// Prints: { 1 2 30 4 5 6 70 8 9 10 110 12 13}
v[slice(3, 4, 2)] = -1;
cout << v << '\n';
// Prints: { 1 2 30 -1 5 -1 70 -1 9 -1 110 12 13}
valarray<int> mult(3, 2);
v[slice(8, 2, 3)] *= mult;
cout << v << '\n';
// Prints: { 1 2 30 -1 5 -1 70 -1 27 -1 110 36 13}
cout << static_cast<valarray<int> >(v[slice(1, 5, 2)])
<< '\n';
// Prints: { 2 -1 -1 -1 -1}
cout << static_cast<valarray<int> >(v[slice(4, 3, 2)]) +
static_cast<valarray<int> >(v[slice(2, 3, 2)])
<< '\n';
// Prints: { 35 75 97}
}
The members of slice_array are straightforward. When using any of the assignment operators, the valarray on the righthand side must be the same size as the slice_array on the lefthand side. You can also assign a scalar to every element of the array. Note that the default constructor, copy constructor, and copy assignment operator are all private. The purpose of this is to restrict the use of slice_array so it can be used only as a return value from valarray's operator[]. See Alsogslice_array class template, indirect_array class template, mask_array class template, slice class, valarray class template
The sqrt function computes the square root of the elements of a. See Alsosqrt in <cmath>
The tan function computes the tangent of the elements of a. See Alsotan in <cmath>
The tanh function computes the hyperbolic tangent of the elements of a. See Alsotanh in <cmath>
The valarray class template represents an array of numeric values, with restrictions that permit an implementation to optimize performance. In particular, an object cannot be an element of more than one array. A subset, such as a generalized slice or indirect array, cannot specify a single element more than once, or else the behavior is undefined. You can instantiate valarray with any numerical type as its template parameter if you limit yourself to using only operations that are defined for that type. For example, you cannot use operator<< on valarray<double> because you cannot use operator<< on scalars of type double. Examples of using valarray can be found throughout this section. The following are the members of valarray:
See Alsogslice class, gslice_array class template, indirect_array class template, mask_array class template, slice class, slice_array class template |
|
|
|