13.10 <cmath>
The <cmath> header declares a number of mathematical
functions (from the C standard <math.h>). In
addition to the standard C function, most functions have overloaded
versions for different parameter types; each
function's syntax shows all the overloaded versions.
If an argument is out of range, a domain error occurs. The function
sets errno to EDOM and returns
an error value. The value is defined by the implementation, so the
only portable way to test for a domain error is to check
errno. If the function's result
is an overflow, a range error occurs. The function returns
HUGE_VAL and sets errno to
ERANGE. If underflow occurs, the function returns
0 and may or may not set errno
to ERANGE. (See <cerrno>
for more information about errno.)
 |
HUGE_VAL is defined to be a
double, and the C++ standard does not define a
suitable value for the float and
long double versions of the
math functions. If you are using a system that has infinity as an
explicit floating-point value (such as IEC 60559/IEEE 754, which is
found on PCs, Macintoshes, and modern workstations), the overloaded
versions of a function probably return infinity for overflow, so
there is no problem with the float and
long double versions of the
functions. For maximum portability, however, use only the
double versions of the math functions.
|
|
All the trigonometric functions use radians. The descriptions of
these functions use the common mathematical notation for ranges of
values. [x, y) represents
all values z such that x
 z <
y—that is, the square bracket denotes an
inclusive endpoint of a range, and the parenthesis denotes an
exclusive endpoint of a range. z <
y—that is, the square bracket denotes an
inclusive endpoint of a range, and the parenthesis denotes an
exclusive endpoint of a range.
Several other headers in the standard library declare additional
mathematical functions:
- <cfloat>
-
Declares macros for the limits of floating-point types
- <climits>
-
Declares macros for the limits of integer types
- <complex>
-
Declares types and functions for working with complex numbers
- <cstdlib>
-
Declares integer absolute value functions and functions that compute
a quotient and remainder in a single operation
- <limits>
-
Declares the numeric_limits class template for the
limits of the numerical types—e.g., the largest
float, the precision of double,
and so on
- <numeric>
-
Declares generic numerical algorithms
- <valarray>
-
Declares types and functions for computation with arrays of numbers
| abs function |
Computes absolute value
|
float abs(float x)
double abs(double x)
long double abs(long double x)
|
|
The abs function returns the absolute value of its
argument: if x < 0, it returns
-x; otherwise, it returns x.
The abs function in
<cmath> is the same as
fabs. The <cstdlib>
header declares integer versions of the abs
function.
See Also
fabs function, abs function in
<cstdlib>
| acos function |
Computes inverse cosine
|
float acos(float x)
double acos(double x)
long double acos(long double x)
|
|
The acos function returns the inverse cosine of
its argument. The parameter x must be in the range
[-1, 1], or a domain error occurs. The return value is in the range
[0, 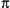 ]. ].
| asin function |
Computes inverse sine
|
float asin(float x)
double asin(double x)
long double asin(long double x)
|
|
The asin function returns the inverse sine of its
argument. The parameter x must be in the range
[-1, 1], or a domain error occurs. The return value is in the range
[-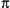 /2, /2, 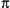 /2]. /2].
| atan function |
Computes inverse tangent
|
float atan(float x)
double atan(double x)
long double atan(long double x)
|
|
The atan function returns the inverse tangent of
its argument. The return value is in the range [-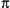 /2, /2,
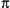 /2]. /2].
| atan2 function |
Computes inverse tangent
|
float atan2(float y, float x)
double atan2(double y, double x)
long double atan2(long double y, long double x)
|
|
The atan2 function returns the inverse tangent of
y/x using the sign of both numbers to determine
the quadrant for the return value. It correctly handles the case in
which x is 0. (That is, it
returns 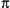 /2 times the sign of y for
nonzero y; if y is
0, the result is implementation-defined and might
be a range error). The return value is in the range [- /2 times the sign of y for
nonzero y; if y is
0, the result is implementation-defined and might
be a range error). The return value is in the range [-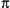 , ,
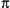 ]. ].
| ceil function |
Computes ceiling
|
float ceil(float x)
double ceil(double x)
long double ceil(long double x)
|
|
The ceil function returns the smallest integer
that is greater than or equal to x.
See Also
floor function
| cos function |
Computes cosine
|
float cos(float x)
double cos(double x)
long double cos(long double x)
|
|
The cos function returns the cosine of its
argument, in radians. The return value is in the range [-1, 1].
| cosh function |
Computes hyperbolic cosine
|
float cosh(float x)
double cosh(double x)
long double cosh(long double x)
|
|
The cosh function returns the hyperbolic cosine of
its argument. Note that <cmath> has no
inverse hyperbolic trigonometric functions; the Boost project fills
that gap. See Appendix B for information about
Boost.
| exp function |
Computes exponential
|
float exp(float x)
double exp(double x)
long double exp(long double x)
|
|
The exp function returns
ex. If x
is too large, a range error occurs.
See Also
log function, pow function
| fabs function |
Computes absolute value
|
float fabs(float x)
double fabs(double x)
long double fabs(long double x)
|
|
The fabs function returns the absolute value of
its argument: if x < 0, it returns
-x; otherwise, it returns x.
The fabs function is the same as
abs for floating-point numbers. It exists only for
compatibility with C.
See Also
abs function, abs function in
<cstdlib>
| floor function |
Computes floor
|
float floor(float x)
double floor(double x)
long double floor(long double x)
|
|
The floor function returns the largest integer
that is less than or equal to x.
See Also
ceil function
| fmod function |
Computes modulus
|
float fmod(float x, float y)
double fmod(double x, double y)
long double fmod(long double x, long double y)
|
|
The fmod function returns the floating-point
remainder of dividing x by y.
If y is 0, the behavior is
implementation-defined: the return value might be
0, or a domain error can occur. If
y is nonzero, the return value is
x - k x
y for some integer k, such
that the result has the same sign as x and an
absolute value less than the absolute value of y.
| frexp function |
Computes binary fraction and exponent
|
float frexp(float x, int* exp)
double frexp(double x, int* exp)
long double frexp(long double x, int* exp)
|
|
The frexp function separates a floating-point
number into a fraction and an exponent (with a base of 2) such that
x = frac x
2e, in which
frac is in the range [1/2, 1) or is
0 if x is 0.
The exponent, e, is stored in
*exp. The return value is
frac. If x is
0, the return value and *exp
are 0.
See Also
ldexp function, modf function
| HUGE_VAL macro |
Range error value
|
When an overflow occurs, most functions set errno
to ERANGE and return HUGE_VAL
with the correct sign of the result. The exact value of
HUGE_VAL is implementation-defined and is not
necessarily a compile-time constant. It might even be a value that
can be returned as a valid result from the function. In that case,
the only way to discover whether an overflow occurred is to test
errno, as shown in Example 13-5.
Example
Example 13-5. Computing a logarithm to any base
// Return the logarithm of x to the base n.
template<typename T>
T logn(T x, T n)
{
errno = 0;
T logx = log(x);
if (errno == ERANGE)
return logx; // Should be HUGE_VAL
else if (errno != 0)
return logx; // Implementation defined
T logn = log(n);
if (errno == ERANGE)
return logn; // Should be HUGE_VAL
else if (errno != 0)
return logn; // Implementation defined
if (logn == 0) {
errno = EDOM;
return 0;
}
return logx / logn;
}
See Also
<cerrno>
| ldexp function |
Makes floating point from binary fraction and exponent
|
float ldexp(float frac, int exp)
double ldexp(double frac, int exp)
long double ldexp(long double frac, int exp)
|
|
The ldexp function returns a floating-point number
that it constructs from a fractional part and an exponent (base 2).
The return value is frac x
2exp.
See Also
frexp function, modf function
| log function |
Computes natural logarithm
|
float log(float x)
double log(double x)
long double log(long double x)
|
|
The log function returns the natural (base
e) logarithm of its argument. A domain error
occurs if x is negative. A range error might occur
if x is 0.
| log10 function |
Computes common logarithm
|
float log10(float x)
double log10(double x)
long double log10(long double x)
|
|
The log10 function returns the common (base 10)
logarithm of its argument. A domain error occurs if
x is negative. A range error might occur if
x is 0.
| modf function |
Separates integer and fraction parts
|
float modf(float x, float* iptr)
double modf(double x, double* iptr)
long double modf(long double x, long double* iptr)
|
|
The modf function splits a floating-point number
into integral and fractional parts. Both parts have the same sign as
x. The integral part is stored in
*iptr; the return value is the fractional part.
See Also
frexp function, ldexp function
| pow function |
Computes power
|
float pow(float x, float y)
float pow(float x, int y)
double pow(double x, double y)
double pow(double x, int y)
long double pow(long double x, long double y)
long double pow(long double x, int y)
|
|
The pow function raises x to
the y power. If x is negative,
and y is not an integral value, a domain error
occurs. If x is 0, and
y is less than or equal to 0,
and the result cannot be represented as a real number, a domain error
occurs. A range error can occur if the result is out of range.
See Also
exp function
| sin function |
Computes sine
|
float sin(float x)
double sin(double x)
long double sin(long double x)
|
|
The sin function returns the sine of its argument,
in radians. The return value is in the range [-1, 1].
| sinh function |
Computes hyperbolic sine
|
float sinh(float x)
double sinh(double x)
long double sinh(long double x)
|
|
The sinh function returns the hyperbolic sine of
its argument. Note that <cmath> has no
inverse hyperbolic trigonometric functions; the Boost project fills
that gap. See Appendix B for information about
Boost.
| sqrt function |
Computes square root
|
float sqrt(float x)
double sqrt(double x)
long double sqrt(long double x)
|
|
The sqrt function returns the square root or its
argument. If x is negative, a domain error occurs.
The return value is always positive or 0.
| tan function |
Computes tangent
|
float tan(float x)
double tan(double x)
long double tan(long double x)
|
|
The tan function returns the tangent of its
argument. The standard does not specify the result when the tangent
is undefined (that is, when x is
k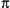 + +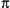 /2 for any integer
k), but a reasonable result is a range error.
Due to the nature of the tangent function, the sign of the return
value (HUGE_VAL) can be positive or negative. /2 for any integer
k), but a reasonable result is a range error.
Due to the nature of the tangent function, the sign of the return
value (HUGE_VAL) can be positive or negative.
| tanh function |
Computes hyperbolic tangent
|
float tanh(float x)
double tanh(double x)
long double tanh(long double x)
|
|
The tanh function returns the hyperbolic tangent
of its argument. Note that <cmath> has no
inverse hyperbolic trigonometric functions; the Boost project fills
that gap. See Appendix B for information about
Boost.
|