13.11 <complex>
The <complex> header declares the
complex class template and specializations for the
float, double, and
long double types. It also
declares mathematical functions that work with
complex values.
| abs function template |
Computes absolute value
|
template<typename T> T abs(const complex<T>& z)
|
|
The abs function returns the absolute value (or
magnitude) of z.
See Also
polar function template, abs
function in <cmath>
| arg function template |
Computes argument (angle)
|
template<typename T> T arg(const complex<T>& z)
|
|
The arg function returns the argument (angle in
polar coordinates) of z.
See Also
polar function template
| complex class template |
Complex number template
|
template<typename T>
class complex {
public:
typedef T value_type;
complex(const T& re = T( ), const T& im = T( ));
complex(const complex& z);
template<typename X> complex(const complex<X>& z);
T real( ) const;
T imag( ) const;
complex& operator= (const T& x);
complex& operator+=(const T& x);
complex& operator-=(const T& x);
complex& operator*=(const T& x);
complex& operator/=(const T& x);
complex& operator=(const complex& z);
template<typename X>
complex& operator= (const complex<X>& z);
template<typename X>
complex& operator+=(const complex<X>& z);
template<typename X>
complex& operator-=(const complex<X>& z);
template<typename X>
complex& operator*=(const complex<X>& z);
template<typename X>
complex& operator/=(const complex<X>& z);
};
|
|
The complex class template represents a complex
number. The <complex> header specializes the
template for the float, double,
and long double types. You can
instantiate complex<> for any type that
behaves in the manner of the fundamental numeric types.
The type definition is a straightforward representation of a complex
number. Basic assignment operators are defined as member functions,
and arithmetic operators are defined as global functions.
- template<typename X> complex(const complex<X>& z)
-
Constructs a complex<T> object by copying
the members from z. Effectively, this converts a
complex object instantiated for one type to a
complex object of another type.
- T real( ) const
-
Returns the real part of *this.
- T imag( ) const
-
Returns the imaginary part of *this.
- complex& operator=(const T& x)
-
Assigns x to the real part of
*this and 0 to the imaginary
part. Returns *this.
- complex& operator+=(const T& x)
-
Adds x to the real part of
*this, leaving the imaginary part alone. Returns
*this.
- complex& operator-=(const T& x)
-
Subtracts x from the real part of
*this, leaving the imaginary part alone. Returns
*this.
- complex& operator*=(const T& x)
-
Multiplies the real and imaginary parts of *this
by x. Returns *this.
- complex& operator/=(const T& x)
-
Divides the real and imaginary parts of *this by
x. Returns *this.
- complex& operator=(const complex& z)
-
Assigns the real and imaginary parts of z to
*this. Returns *this.
- template<typename X> complex& operator=(const complex<X>& z)
-
Assigns the real and imaginary parts of z to
*this. Returns *this. Note that
z and *this can have different
template parameter types.
- template<typename X> complex& operator+=(const complex<X>& z)
-
Adds z to *this. Returns
*this. Note that z and
*this can have different template parameter types.
- template<typename X> complex& operator-=(const complex<X>& z)
-
Subtracts z from *this. Returns
*this. Note that z and
*this can have different template parameter types.
- template<typename X> complex& operator*=(const complex<X>& z)
-
Multiplies *this by z. Returns
*this. Note that z and
*this can have different template parameter types.
- template<typename X> complex& operator/=(const complex<X>& z)
-
Divides *this by z. Returns
*this. Note that z and
*this can have different template parameter types.
| complex<double> template specialization |
Double-precision complex number
|
template<> class complex<double> {
public:
typedef double value_type;
complex(double re = 0.0, double im = 0.0);
complex(const complex<float>&);
explicit complex(const complex<long double>&);
double real( ) const;
double imag( ) const;
complex<double>& operator= (double);
complex<double>& operator+=(double);
complex<double>& operator-=(double);
complex<double>& operator*=(double);
complex<double>& operator/=(double);
complex<double>& operator=(const complex<double>&);
template<typename X>
complex<double>& operator= (const complex<X>&);
template<typename X>
complex<double>& operator+=(const complex<X>&);
template<typename X>
complex<double>& operator-=(const complex<X>&);
template<typename X>
complex<double>& operator*=(const complex<X>&);
template<typename X>
complex<double>& operator/=(const complex<X>&);
};
|
|
The complex<double> class is a
straightforward specialization of the complex
class template. It changes the operators to pass
double parameters by value instead of by
reference, and it adds a new constructor:
- explicit complex(const complex<long double>& z)
-
Constructs a complex number by copying from z.
Note that you might lose precision or overflow, so the constructor is
explicit.
| complex<float> template specialization |
Single-precision complex number
|
template<> class complex<float> {
public:
typedef float value_type;
complex(float re = 0.0f, float im = 0.0f);
explicit complex(const complex<double>&);
explicit complex(const complex<long double>&);
float real( ) const;
float imag( ) const;
complex<float>& operator= (float);
complex<float>& operator+=(float);
complex<float>& operator-=(float);
complex<float>& operator*=(float);
complex<float>& operator/=(float);
complex<float>& operator=(const complex<float>&);
template<typename X>
complex<float>& operator= (const complex<X>&);
template<typename X>
complex<float>& operator+=(const complex<X>&);
template<typename X>
complex<float>& operator-=(const complex<X>&);
template<typename X>
complex<float>& operator*=(const complex<X>&);
template<typename X>
complex<float>& operator/=(const complex<X>&);
};
|
|
The complex<float> class is a
straightforward specialization of the complex
class template. It changes the operators to pass
float parameters by value instead of by reference,
and it adds two new constructors:
- explicit complex(const complex<double>& z)
- explicit complex(const complex<long double>& z)
-
Constructs a complex number by copying from z.
Note that you might lose precision or overflow, so the constructors
are explicit.
| complex<long double> template specialization |
Extended-precision complex number
|
template<> class complex<long double> {
public:
typedef long double value_type;
complex(long double re = 0.0L, long double im = 0.0L);
complex(const complex<float>&);
complex(const complex<double>&);
long double real( ) const;
long double imag( ) const;
complex<long double>&
operator=(const complex<long double>&);
complex<long double>& operator= (long double);
complex<long double>& operator+=(long double);
complex<long double>& operator-=(long double);
complex<long double>& operator*=(long double);
complex<long double>& operator/=(long double);
template<typename X>
complex<long double>& operator= (const complex<X>&);
template<typename X>
complex<long double>& operator+=(const complex<X>&);
template<typename X>
complex<long double>& operator-=(const complex<X>&);
template<typename X>
complex<long double>& operator*=(const complex<X>&);
template<typename X>
complex<long double>& operator/=(const complex<X>&);
};
|
|
The complex<long double> class is a
straightforward specialization of the complex
class template. It changes the operators to pass
long double parameters by value
instead of by reference.
| conj function template |
Computes conjugate
|
template<typename T> complex<T> conj(const complex<T>& z)
|
|
The conj function returns the complex conjugate of
z.
| cos function template |
Computes cosine
|
template<typename T> complex<T> cos(const complex<T>& z)
|
|
The cos function returns the complex cosine of
z.
See Also
cos function in <cmath>
| cosh function template |
Computes hyperbolic cosine
|
template<typename T> complex<T> cosh(const complex<T>& z)
|
|
The cosh function returns the complex hyperbolic
cosine of z.
See Also
cosh function in <cmath>
| exp function template |
Computes exponential
|
template<typename T> complex<T> exp(const complex<T>& z)
|
|
The exp function returns the exponential of
z, that is,
ez.
See Also
exp function in <cmath>
| imag function template |
Returns imaginary part
|
template<typename T> T imag(const complex<T>& z)
|
|
The imag function returns the imaginary part of
z, that is, z.imag( ).
See Also
abs function in <cmath>
| log function template |
Computes natural logarithm
|
template<typename T> complex<T> log(const complex<T>& z)
|
|
The log function returns the complex natural (base
e) logarithm of z. The branch
cuts are along the negative real axis, which means the imaginary part
of the result is in the range [-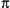 i, i,
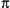 i]. i].
See Also
log function in <cmath>
| log10 function template |
Computes common logarithm
|
template<typename T> complex<T> log10(const complex<T>& z)
|
|
The log10 function returns the complex common
(base 10) logarithm of z. The branch cuts are
along the negative real axis, which means the imaginary part of the
result is in the range [-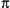 i, i,
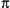 i]. i].
See Also
log10 function in <cmath>
| norm function template |
Computes normalized value
|
template<typename T> T norm(const complex<T>& z)
|
|
The norm function returns the square of the
absolute value of z.
See Also
abs function template
| operator+ function template |
Persforms unary positive or addition
|
template<typename T>
complex<T> operator+(const complex<T>& z);
template<typename T> complex<T>
operator+(const complex<T>& x, const complex<T>& y);
template<typename T> complex<T>
operator+(const complex<T>& x, const T& y);
template<typename T> complex<T>
operator+(const T& x, const complex<T>& y);
|
|
The unary positive operator returns z.
The binary addition operator returns the sum of its operands. If
either operand is of type T, the argument is
interpreted as the real part, with an imaginary part of T(
) or 0.
| operator- function template |
Performs negation or subtraction
|
template<typename T>
complex<T> operator-(const complex<T>&);
template<typename T>
complex<T> operator-(const complex<T>&, const complex<T>&);
template<typename T>
complex<T> operator-(const complex<T>&, const T&);
template<typename T>
complex<T> operator-(const T&, const complex<T>&);
|
|
The unary negation operator returns -z.
The binary subtraction operator returns the difference of its
operands. If either operand is of type T, the
argument is interpreted as the real part, with an imaginary part of
T( ) or 0.
| operator* function template |
Performs multiplication
|
template<typename T>
complex<T> operator*(const complex<T>&, const complex<T>&);
template<typename T>
complex<T> operator*(const complex<T>&, const T&);
template<typename T>
complex<T> operator*(const T&, const complex<T>&);
|
|
The binary * operator performs complex
multiplication. If either operand is of type T,
the argument is interpreted as the real part, with an imaginary part
of T( ) or 0.
| operator/ function template |
Performs division
|
template<typename T>
complex<T> operator/(const complex<T>&, const complex<T>&);
template<typename T>
complex<T> operator/(const complex<T>&, const T&);
template<typename T>
complex<T> operator/(const T&, const complex<T>&);
|
|
The binary / operator performs complex division.
If either operand is of type T, the argument is
interpreted as the real part, with an imaginary part of T(
) or 0. Division by zero results in
undefined behavior.
| operator== function template |
Checks equality
|
template<typename T>
bool operator==(const complex<T>&, const complex<T>&);
template<typename T>
bool operator==(const complex<T>&, const T&);
template<typename T>
bool operator==(const T&, const complex<T>&);
|
|
The == operator returns true if
the real and imaginary parts of both values are equal. If either
operand is of type T, the argument is interpreted
as the real part, with an imaginary part of T( )
or 0.
| operator!= function template |
Checks inequality
|
template<typename T>
bool operator!=(const complex<T>&, const complex<T>&);
template<typename T>
bool operator!=(const complex<T>&, const T&);
template<typename T>
bool operator!=(const T&, const complex<T>&);
|
|
The != operator returns true if
the real or imaginary parts are not equal. If either operand is of
type T, the parameter is interpreted as the real
part, with an imaginary part of T( ) or
0.
| operator<< function template |
Writes a complex number
|
template<typename T, typename charT, typename traits>
basic_ostream<charT, traits>& operator<<(basic_ostream<charT, traits>&,
const complex<T>& z);
|
|
The << operator prints z
to the output stream in the form (x, y), in which
x is the real part, and y is
the imaginary part. Example 13-6 shows how
z is formatted. If you want more control over the
formatting, you must print the value yourself.
Example
Example 13-6. Formatting a complex number
template<class T, class charT, class traits>
std::basic_ostream<charT, traits>&
operator<<(std::basic_ostream<charT, traits>& o,
const std::complex<T>& x)
{
std::basic_ostringstream<charT, traits> s;
s.flags(o.flags( ));
s.imbue(o.getloc( ));
s.precision(o.precision( ));
s << "(" << x.real( ) << "," << x.imag( ) << ")";
return o << s.str( );
}
| operator>> function template |
Reads a complex number
|
template<typename T, typename charT, typename traits>
basic_istream<charT, traits>& operator>>(basic_istream<charT, traits>&,
complex<T>& z);
|
|
The >> operator reads a complex number from
an input stream into z. The input format can be
any of the following:
- x
-
The value x is the real part, and T(
) or 0 is the imaginary part.
- (x)
-
The value x is the real part, and T(
) or 0 is the imaginary part.
- (x, y)
-
The value x is the real part, and
y is the imaginary part.
| polar function template |
Converts to polar coordinates
|
template<typename T>
complex<T> polar(const T& r, const T& theta)
|
|
The polar function returns a complex object that
represents the value given in polar coordinates, in which
r is the magnitude and theta is
the angle (in radians). The resulting value has the following real
and imaginary parts:
real = r * cos(theta)
imag = r * sin(theta)
See Also
abs function template, arg
function template
| pow function template |
Computes power
|
template<class T>
complex<T> pow(const complex<T>& x, int y);
template<class T>
complex<T> pow(const complex<T>& x, const T& y);
template<class T>
complex<T> pow(const complex<T>& x, const complex<T>& y);
template<class T>
complex<T> pow(const T& x, const complex<T>& y);
|
|
The pow function returns the complex power
xy. If x and
y are both 0, the result is
implementation-defined; otherwise, the result is
exp(y *
log(x)). The branch cuts are along the negative
real axis.
See Also
exp function template, log
function template, pow function in
<cmath>
| real function template |
Returns real part
|
template<typename T> T real(const complex<T>& z)
|
|
The real function returns the real part of
z, that is, z.real( ).
| sin function template |
Computes sine
|
template<typename T> complex<T> sin(const complex<T>& z)
|
|
The sin function returns the complex sine of
z.
See Also
sin function in <cmath>
| sinh function template |
Computes hyperbolic sine
|
template<typename T> complex<T> sinh(const complex<T>& z)
|
|
The sinh function returns the complex hyperbolic
sine of z.
See Also
sinh function in <cmath>
| sqrt function template |
Computes square root
|
template<typename T> complex<T> sqrt(const complex<T>& z)
|
|
The sqrt function returns the complex square root
of z.The branch cuts are along the negative real
axis. The result always has a nonnegative real part.
See Also
sqrt function in <cmath>
| tan function template |
Computes tangent
|
template<typename T> complex<T> tan(const complex<T>& z)
|
|
The tan function returns the complex tangent of
z.
See Also
tan function in <cmath>
| tanh function template |
Computes hyperbolic tangent
|
template<typename T> complex<T> tanh(const complex<T>& z)
|
|
The tanh function returns the complex hyperbolic
tangent of z.
See Also
tanh function in
<cmath>
|