บทที่ 1 การเคลื่อนที่ในแนวเส้นตรง

 

เนื้อหาประกอบด้วย

1.1    คำจำกัดความของตำแหน่งและการกระจัด

1.2    คำจำกัดความของความเร็วเฉลี่ย

1.3    คำจำกัดความของความเร็วขณะใดขณะหนึ่งและอัตราเร็ว

1.4    คำจำกัดความของความเร่งเฉลี่ยและความเร่งขณะใดขณะหนึ่ง

1.5    การเคลื่อนที่เมื่อความเร่งคงที่

1.6    การตกอิสระของวัตถุ

1.7    สมการจลศาสตร์และการแก้สมการโดยใช้แคลลูลัส

 

ในบทนี้จะศึกษาเกี่ยวกับการเคลื่อนที่ของวัตถุใน 1  มิติ  โดยไม่สนใจถึงสาเหตุที่ทำให้วัตถุเคลื่อนที่เรียกว่า  จลศาสตร์

 

1.1                    คำจำกัดความของตำแหน่งและการกระจัด

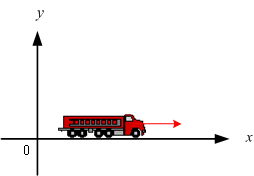
ก่อนจะทำความเข้าใจเรื่องต่าง ๆ ในหัวข้อต่อ ๆ ไป ต้องทราบความหมายตำแหน่งของวัตถุก่อน   พิจารณารูปที่  1.1

 

 

 

 

 

 

 

 

 

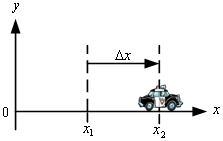
               รูปที่  1.1                                              รูปที่ 1.2

 

ตำแหน่ง  คือบริเวณที่ตั้งของวัตถุ (รถตั้งอยู่ที่ตำแหน่ง  ) ในระบบพิกัดฉาก

การกระจัด คือการเปลี่ยนแปลงตำแหน่งของวัตถุ พิจารูปที่ 1.2 เมื่อรถเปลี่ยนตำแหน่งจาก  ไปยัง ตำแหน่ง จากเงื่อนไขข้างต้นสามารถนำมาเขียนเป็นสมการทางคณิตศาสตร์ได้ดังนี้

                                      ตำแหน่ง   

                                      นิยามการกระจัด

ตัวอย่างที่ 1.1 จากรูปเป็นกราฟการเดินทางท่องเที่ยวไปเชียงใหม่โดยทางรถยนต์  เมื่อจุดเริ่มต้นอยู่ที่มหาวิทยาลัยรังสิต  ดังรูปที่ 1.2 จงคำนวณหา

 

 

 

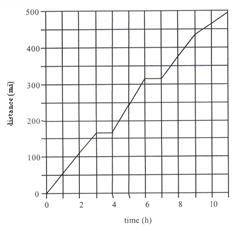ก.     ตำแหน่งของรถยนต์ที่ 

ข.     ตำแหน่งของรถยนต์ที่ 

ค.     การกระจัดภายในเวลา 

ง.      การกระจัดทั้งหมด

 

 

 

 

 

 

 รูปที่  1. 2

วิธีทำ

          ก. จากกราฟ  

                 ข. จากกราฟ   

                 ค. จากคำจำกัดความของการกระจัด                 

=      

=      

          ง. จากกราฟการกระจัดทั้งหมด                =      

 

1.2                    คำจำกัดความของความเร็วเฉลี่ย

จากหัวข้อที่  1.1   เมื่อทราบตำแหน่งของวัตถุแล้วในหัวข้อต่อไปจะอธิบายถึงการเปลี่ยนแปลงตำแหน่งอย่างรวดเร็ว

ความเร็วเฉลี่ย   คืออัตราการเปลี่ยนแปลงการกระจัดต่อช่วงเวลา 

คำจำกัดความของความเร็วเฉลี่ยเมื่อเขียนในรูปของสมการทางคณิตศาสตร์

                       

 

ตัวอย่างที่ 1.2  จากโจทย์ข้อ 1.1 จงคำนวณหา

ก.     ความเร็วเฉลี่ยในการเดินทางจาก  ถึง

ข.     ความเร็วเฉลี่ยเมื่อสิ้นสุดการเดินทาง

 

วิธีทำ   จากคำจำกัดความของความเร็วเฉลี่ย

          ก.                       =            =      

                                      =      

                                       =      

                                  =       ข.                 

                               =            =      

                                      =      

                                              =      

 

จากตัวอย่างข้างต้นแสดงให้เห็นถึงการเลื่อนตำแหน่ง  พิจารณาการเคลื่อนตำแหน่งของวัตถุภายในเวลา  2 ชั่วโมง  จากช่วงเวลา     ถึง    และจาก  ถึง  ความเร็วเฉลี่ยภายในช่วงเวลา  2 ชั่วโมงในกรณีเช่นนี้หาไม่ได้เนื่องจากช่วงเวลาไม่ต่อเนื่อง

 

 

 

 

 

 

 

 

 

 

1.3                    นิยามความเร็วขณะใดขณะหนึ่งและอัตราเร็ว

 

 

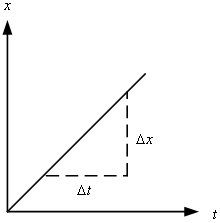
จากรูปที่ 1.3 กราฟแสดงความสัมพันธ์ระหว่าง ตำแหน่งกับเวลา เป็นกราฟเส้นตรงความเร็วเฉลี่ยคือความชัน (slope) ของกราฟ

เนื่องจาก

                   

      อัตราเร็วเฉลี่ย คือขนาดของเร็วเฉลี่ย เป็นการกระจัดต่อช่วงเวลา

 

 

 

 

รูปที่  1.3

 

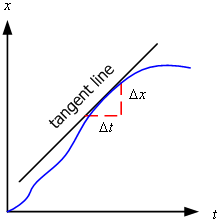
          จากรูปที่ 1.4 กราฟแสดงความสัมพันธ์ระหว่าง ตำแหน่งกับเวลา เป็นกราฟเส้นโค้ง  ความเร็วเฉลี่ย (ความชัน) จะมีการเปลี่ยนแปลงขึ้นอยู่กับขนาดของ   ถ้า  มีค่าน้อยมาก ๆ  เราสามารถหา ความชัน ได้จากเส้นสัมผัส (tangent line) ส่วนโค้ง  ความเร็วทีได้เรียกว่าความเร็วขณะใดขณะหนึ่งนั่นคือ

                          =      

สามารถเขียนอยู่ในรูปของสมการทางคณิตศาสตร์ได้ดังนี้

 

                    รูปที่  1.4                                            =      

         

 

 

 

นั่นคือความเร็วขณะใดขณะหนึ่งเป็นการกระจัดต่อเวลาในช่วงเวลาสั้นมาก ๆ หรือเป็นความเร็วที่จุดใดจุดหนึ่งของการเคลื่อนที่ เช่นความเร็วขณะขับรถสังเกตุได้จากเข็มไมล์ขณะนั้น ดังรูปที่ 1.5

 

 

 

 

รูปที่ 1.5

 

 

 

ตัวอย่างที่ 1.3 โยนลูกบอลขึ้นตามแนวดิ่งตำแหน่งของลูกบอล ณ.เวลา  ใด ๆ คือ   

ก.     จงเขียนกราฟแสดงความสัมพันธ์ระหว่างเวลากับระยะทาง

ข.     ความเร็วเฉลี่ยในช่วง 2 วินาทีแรก

ค.     ความเร็วเฉลี่ยในช่วง 1 วินาทีแรก

ง.      ความเร็วที่เวลา 

วิธีทำ

ก.

 

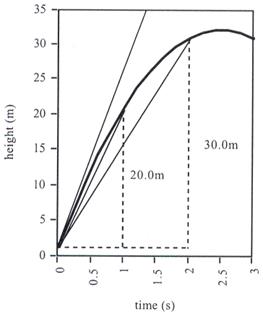ข.     จากคำจำกัดความของความเร็วเฉลี่ย

       =      

      =                    =      

      =                    =      

                 =      

                 =      

                 =              =      

ค.     จากคำจำกัดความของความเร็วเฉลี่ย

       =      

      =             =        

      =         =      

                 =      

                 =      

                 =           =      

 

ง.      ความเร็วที่    คือความเร็วขณะใดขณะหนึ่งจะได้

       =        

          =      

เมื่อ  

                          =        

                             =      

 

ข้อสังเกต   จากตัวอย่างข้างต้นสังเกตได้ว่าในขณะที่ช่วงเวลาสั้นลงความเร็วเฉลี่ยจะมีค่าใกล้กับความเร็วขณะใดขณะหนึ่ง 

คำจำกัดความของอัตราเร็วคือขนาดของความเร็วขณะใดขณะหนึ่ง  อัตราเร็วจะมีค่าเป็นบวกเสมอ  ในขณะที่ความเร็วมีได้ทั้งค่าบวกและค่าลบ  ข้อแตกต่างระหว่างอัตราเร็วและความเร็วจะสังเกตเห็นได้ง่ายขึ้น  เมื่อความเร็วคิดอยู่ในรูปของเวกเตอร์ซึ่งจะศึกษาไปในการเคลื่อนที่  2 มิติ

 

1.4                    คำจำกัดความของความเร่งเฉลี่ยและความเร่งขณะใดขณะหนึ่ง

          ในหัวข้อนี้จะอธิบายถึงการเปลี่ยนแปลงความเร็วซึ่งเรียกว่าความเร่ง ข้อแตกต่างระหว่างความเร็วและความเร่งคือ  ความเร็วบอกถึงการเปลี่ยนแปลงตำแหน่ง  ส่วนความเร่งบอกถึงการเปลี่ยนแปลงความเร็วนั่นคือความเร่งคืออัตราการเปลี่ยนแปลงความเร็ว 

     เมื่อเขียนอยู่ในรูปสมการทางคณิตศาสตร์จะได้นิยามของความเร่งเฉลี่ยคือ

                               =      

     คำจำกัดความของความเร่งขณะใดขณะหนึ่ง

                               =      

 

ตัวอย่างที่ 1.4 รถยนต์คันหนึ่งสามารถเร่งความเร็วจาก    จนกระทั่งมีความเร็ว    ภายในเวลา   จงหาความเร่งเฉลี่ยของรถคันนี้

วิธีทำ  จาก                     =      

                                      =      

                                      =      

 

          จากกราฟแสดงความสัมพันธ์ระหว่างตำแหน่งกับเวลา  ความชันของกราฟคือความเร็ว  ในทำนองเดียวกันความเร่งคือความชันของกราฟแสดงความสัมพันธ์ระหว่างความเร็วกับเวลา

 

ตัวอย่างที่  1.5      กราฟแสดงความสัมพันธ์ระหว่างความเร็วกับเวลาของรถคันหนึ่งแสดงดังรูปที่ 1.6 จากกราฟอธิบายว่าเมื่อ 

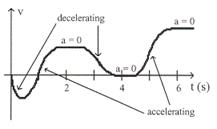
ก.     ช่วงแรกรถมีความหน่วง (decelerating) 

ข.     รถมีความเร่ง  (accelerating)

ค.     ความเร่งเป็นศูนย์ 

ง.      รถมีความเร็วลดลง

 

 

               รูปที่  1.6

วิธีทำ    ก. ; ข. ; ค.  จากคำจำกัดความของความเร่งขณะใดขณะหนึ่ง   ซึ่งสามารถหาได้จากความชันของกราฟ

          ง. ช่วงที่รถมีความเร็วลดลงมีอยู่  2  ช่วงคือช่วงเวลา   ถึง  และช่วงเวลา    ถึง  

 

1.5                    การเคลื่อนที่เมื่อความเร่งคงที่

          ถ้าเรารู้ว่าวัตถุเริ่มต้นเคลื่อนที่จากตำแหน่งไหน  ความเร็วต้นเท่าใดและมีความเร่งเท่าใด  เราจะสามารถบอกได้ว่าช่วงต่อไปวัตถุจะอยู่ที่ไหน  ปัญหาที่เกิดขึ้นนี้สามารถอธิบายได้โดยใช้สมการทางคณิตศาสตร์ เมื่อกำหนดให้ตำแหน่งเริ่มต้นคือ ; ความเร็วต้นคือ ; ความเร่งคือ  ความเร่งเมื่อเป็นฟังก์ชั่นของเวลาคือ  ; ความเร็วเมื่อเป็นฟังก์ชั่นของเวลาคือ  ; ตำแหน่งเมื่อเป็นฟังก์ชั่นของเวลาคือ  ; ความเร่งเมื่อเป็นฟังก์ชั่นของตำแหน่งคือ  ; และความเร็วเมื่อเป็นฟังก์ชั่นของตำแหน่งคือ   ซึ่งสามารถเขียนอยู่ในรูปสมการการเคลื่อนที่

ในกรณีที่วัตถุเคลื่อนที่ด้วยความเร่งคงที่สมการการเคลื่อนที่กรณีนี้ เราเรียกว่าสมการจลศาสตร์ ให้   ;  ;  เมื่อ  คือความเร่งคงที่

สมการความเร็วเมื่อเป็นฟังก์ชั่นของเวลาพิจารณาได้จากนิยามความเร่งเฉลี่ย

                               =      

                               =      

                              =        

เป็นสมการความเร็วเมื่อเป็นฟังก์ชั่นของเวลา

 

สมการตำแหน่งเมื่อเป็นฟังก์ชั่นของเวลาพิจารณาได้จากนิยามความเร็วเฉลี่ย

                               =      

                    =      

                                  =      

แทน  ด้วย  จากสมการข้างบนซึ่งเป็นสมการความเร็วเมื่อฟังก์ชั่นของเวลาจะได้

                                  =      

                                  =      

                              =      

เป็นสมการตำแหน่งเมื่อเป็นฟังก์ชั่นของเวลา

 

     ในทำนองเดียวกันความเร็วเมื่อเป็นฟังก์ชั่นของตำแหน่ง  สามารถหาได้โดยหาเวลาจากสมการความเร็วที่เป็นฟังก์ชั่นของเวลา   จากนั้นนำเวลาที่ได้แทนลงในสมการตำแหน่งเมื่อเป็นฟังก์ชั่นของเวลาดังนี้

                              =      

                                =      

จาก                               =      

                                      =      

                                      =      

                                      =      

                                  =      

                              =      

 

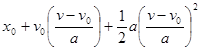
จากสมการจะเห็นว่าเมื่อ   คงที่ความเร็วจะเป็นฟังก์ชั่นของระยะทางเขียนใหม่ได้เป็น

                                   =      

 

จากสมการที่ได้กำหนดให้   คือตำแหน่งเริ่มต้น ;  คือความเร็วต้น ;  คือความเร่งเป็นค่าคงที่   เราสามารถใช้สมการเหล่านี้หาความเร่ง  ความเร็ว  และตำแหน่งของวัตถุที่เวลาใด ๆได้และยังสามารถหาความเร่งและความเร็วของวัตถุที่ตำแหน่งใด ๆ ได้

 

สมการการเคลื่อนที่ของวัตถุเมื่อความเร่งคงที่สามารถเขียนได้ดังนี้

                                   =      

                                   =      

                                   =      

                                   =      

                                   =      

 

          บางกรณีในสมการจลศาสตร์เราไม่ทราบตำแหน่งเริ่มต้น  ความเร็วต้น หรือค่าต่าง ๆ เพื่อความสะดวกในการใช้เราสมารถนำมาเขียนเพื่อแสดงค่าที่ไม่ปรากฎได้ดังนี้

 

 

สมการจลศาสตร์	ค่าที่ไม่ปรากฏ

 

 

          จากห้าสมการที่ได้จะสังเกตได้ว่าแต่ละสมการจะมีค่าที่ไม่ปรากฏในแต่ละสมการอยู่ 1 ค่า  จากเงื่อนไขดังกล่าวเราสมารถยุบสมการต่าง ๆ ดังกล่าวให้เหลือเพียง  2 หรือ 3 สมการได้จากนั้นก็ให้แทนค่าที่ไม่ต้องการให้ปรากฏลงในสมการนั่นได้ดังนี้

          กรณียุบให้เหลือเพียง 2 สมการคือ

                                    =      

                                    =      

          เมื่อไม่ต้องการให้มีค่า  ปรากฏในสมการก็ให้แทนค่า  ลงในสมการ   จะได้

                              =      

                                      =      

                                      =      

                             =      

                                      =      

                                      =      

                             =      

                                   =      

 

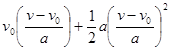
หมายเหตุ     นับเป็นค่าเดียวได้เนื่องจากเราสามารถเลือก   หรือ ได้จากระบบพิกัดแกนมุมฉาก

 

ตัวอย่างที่ 1.6  รถยนต์คันหนึ่งเร่งความเร็วจาก   เป็น  ภายในเวลา  ดังรูปที่ 1.7  จงหา

ก. ความเร่ง

ข. ระยะทางที่รถวิ่งได้ภายในเวลา 6 s.

 

วิธีทำ   ก. จากโจทย์ค่าที่ไม่ปรากฏคือตำแหน่งสุดท้าย  เมื่อ  ;  ;  ;  ;  ;

          จากสมการ

 

                 =      

                 =      

          รูปที่ 1.7                                                   =      

          ข. เมื่อค่าที่ไม่ปรากฏคือความเร่ง

                                       =      

เริ่มต้น   ;  ;

                                             =      

                                                =      

                                                =      

 

1.6                    การตกอิสระของวัตถุ

วัตถุเมื่อตกอย่างอิสระจะมีความเร่ง  เมื่อไม่คิดแรงต้านของอากาศ

หลักการคำนวณ  ใช้สมการจลศาสตร์ดังกล่าวจากข้างต้นเมื่อแทนค่า   ด้วยค่า  การพิจารณาทิศให้พิจารณาตามความเร็วต้น

 

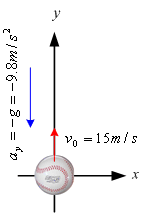
ตัวอย่างที่  1.7  ขว้างลูกบอลขึ้นไปในอากาศด้วยความเร็วต้น  15 (m/s)  ดังรูปที่ 1.8 จงคำนวณหา

           ก. ระยะทางสูงสุดที่ลูกบอลเคลื่อนที่ได้

 ข. เวลาที่ตำแหน่งสูงสุด

วิธีทำ                   

 

ก.  จากโจทย์เมื่อไม่ทราบเวลา  เมื่อ ;   ;  ; ;  จากสมการ

     =       

เริ่มต้น 

ที่ตำแหน่งสูงสุด  

       =                               

       =        

          =         

          =          

 

 

        รูปที่  1.8                                                    

                                                              

ข. จากโจทย์เมื่อไม่ทราบตำแหน่งสุดท้าย

                                    =      

ที่ตำแหน่งสูงสุด

                                     =      

                                      =      

 

 

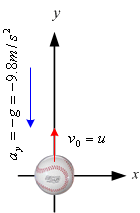
ตัวอย่างที่  1.8  ขว้างลูกบอลขึ้นไปในอากาศด้วยความเร็วต้น   ดังรูปที่  1.9 

ก.จงแสดงให้เห็นว่าเวลาที่ใช้ในการเคลื่อนที่ถึงตำแหน่งสูงสุด มีค่าเท่ากับเวลาที่ใช้เคลื่อนที่กลับสู่ตำแหน่งเดิม

ข. ความเร็วปลายเมื่อเคลื่อนที่กลับสู่ตำแหน่งเดิม

 

วิธีทำ

ก. จากโจทย์เมื่อไม่ทราบตำแหน่งสุดท้าย เมื่อ  ;   ;  ;  ;

       =                                 

       =      

                =                      

                                                   

หาระยะที่วัตถุขึ้นไปได้สูงสุด  เมื่อไม่ทราบเวลา

                   =      

                 =      

                                     =       

                            

                                                   

 

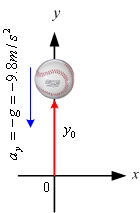
เมื่อตำแหน่งสูงสุดคือระยะเริ่มต้นเมื่อลูกบอลเริ่มตกและ

ความเร็ว ณ. ตำแหน่งนี้คือความเร็วต้นมีค่าเท่ากับศูนย์ จากโจทย์เมื่อไม่ทราบความเร็วสุดท้าย เมื่อ  ;  ;  ;  ;  ;

                           =      

                    =      

      รูปที่  1.9                                 =           

                                                   =      

                                                                  

นั่นคือ                                               =      

 

 

ข. จากโจทย์เมื่อไม่ทราบความเร็วสุดท้าย

                                             =      

                                                =      

                                                =      

นั่นคือความเร็วของลูกบอลขณะกลับสู่ตำแหน่งเดิมจะมีความเร็วเท่ากันแต่ทิศตรงกันข้าม

1.7                    สมการจลศาสตร์และการคำนวณ

            บางครั้งการเคลื่อนที่ของวัตถุถูกกำหนดโดยคำจำกัดความ ของความเร็วและความเร่ง

                               =      

และ                               =      

 

จากสมการข้างต้นเราสามารถใช้แคลลูลัสสร้างสมการจลศาสตร์เมื่อมีความเร่งคงที่ได้

                                    =      

                                   =      

                                =      

ให้  คงที่

                                =      

                               =      

                                    =      

จากสมการที่ได้จะสังเกตุเห็นได้ว่า ความเร็วขึ้นกับเวลา  เขียนใหม่ได้เป็น   ก็คือสมการจลศาสตร์เมื่อความเร็วเป็นฟังก์ชั่นของเวลาในทำนองเดียวกัน

                                   =      

แต่                                =      

                                   =      

                                      =      

                                =      

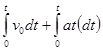
แต่ความเร่ง  และความเร็วต้นไม่เปลี่ยนแปลงตามเวลา

                                =      

                              =      

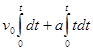
เป็นสมการจลศาสตร์เมื่อตำแหน่งเป็นฟังก์ชั่นของเวลา

          การหาสมการการเคลื่อนที่ของวัตถุ   ดังกล่าวข้างต้นโดยวิธีการหาอนุพันธ์  หรือ          การอินทิเกรต  ใช้สำหรับการหาสมการเมื่อความเร่งไม่คงที่

 

 

 

 

 

 

 

 

 

สรุป

          ในบทนี้สามารถอธิบายการเคลื่อนที่ในรูปของตำแหน่ง  การกระจัด  ความเร็ว  และความเร่ง ในกรณีที่ความเร่งคงที่เราสามารถใช้เงื่อนไขต่าง ๆ สร้างสมการจลศาสตร์ได้  และสามารถใช้คำจำกัดความเบื้องต้นเพื่อหาสมการการเคลื่อนที่เมื่อความเร่งไม่คงที่ได้

ตำแหน่ง   : 

การกระจัด :

ความเร็วเฉลี่ย :

ความเร็วขณะใดขณะหนึ่ง :

ความเร่งเฉลี่ย :

ความเร่งขณะใดขณะหนึ่ง :

 

สมการจลศาสตร์	ค่าที่ไม่ปรากฏ

 

ใช้ในกรณีเมื่อความเร่ง คงที่