บทที่ 13 ความยืดหยุ่น (Elasticity)

          คำจำกัดความ

          เนื่องจากร่างกายมีความยืดหยุ่น จึงทำให้มีการเปลี่ยนแปลงรูปร่างและสามารถกลับเข้าสู่สภาวะเดิมได้  ถ้ามีแรงมากระทำต่อวัตถุเช่นกระดูก วัตถุชนิดนั้นจะเกิดการเปลี่ยน แปลงรูปร่าง (โค้งงอ บิด ยืด หด หรือร้าว เป็นต้น)  เนื่องจากร่างการมีความยืดหยุ่นเมื่อมีแรงมากระทำที่ไม่มากนักร่างกายก็สามารถกลับสู่สภาวะเดิมได้ ในทางตรงกันข้าม ถ้าร่างกายไม่มีความยืดหยุ่น เมื่อมีแรงมากระทำก็จะทำให้หักหรือเปลี่ยนรูปร่าง ในที่นี่อธิบายความยืดหยุ่นเป็นไปตามกฎของฮุค

         

                  

 

 

 

 

 

 

 

 

 

 

 

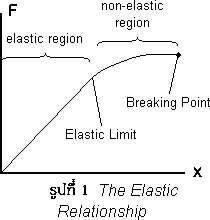
          กฎของฮุค กล่าวว่า “การผิดรูปของวัตถุเป็นปฎิภาคโดยตรงกับแรงที่มากระทำต่อวัตถุนั้น”  เขียนเป็นความสัมพันธ์ได้ดังนี้    เมื่อ    คือผลรวมของการผิดรูป (หด ยืด บิด เป็นต้น)  คือแรงที่กระทำต่อวัตถุนั้น ดังกราฟแสดงความสัมพันธ์ระหว่าง  กับ  สัดส่วนดังกล่าวจะเป็นจริงเฉพาะภายในขอบเขตยืดหยุ่น (elastic region)เท่านั้น กล่าวคือเมื่อแรงมากระทำต่อวัตถุวัตถุสามารถกลับสู่สถานะเดิมได้ ดังรูปที่ 1 นอกเหนือจากขอบเขตนี้ (non-elastic region) วัตถุก็ไม่สามารถกลับมาสู่สถานะเดิมได้จึงถึงจุด breaking point วัตถุจะหัก

          พิจารณากราฟจากรูปที่ 1 เฉพาะในขอบเขตยืดหยุ่นจะได้กราฟความสัมพันธ์เป็นเส้นตรง ความชันของกราฟคือ

                         =            =           =      

          เมื่อ   เป็นค่าคงที่ ของความสัมพันธ์ระหว่าง    เรียกค่า  ว่าค่าคงที่ของสปริง (spring constant)  เขียนเป็นสมการทางคณิตศาสตร์ได้เป็น

                         =      

          เมื่อ   มีหน่วยเป็น  และขึ้นอยู่กับชนิดของวัตถุ วัตถุที่แข็งหรือเปลี่ยนรูปยากจะมีค่าคงที่ของสปริงมาก (ใช้ มากแต่ได้  น้อย) ในทางกลับกันวัตถุที่เปลี่ยน แปลงรูปร่างได้ง่ายจะมีค่าคงที่ของสปริงน้อย

 

          โมดูลัสของความยืดหยุ่น (Modulus of elasticity : E)

          โมดูลัสของความยืดหยุ่น เป็นค่าที่ใช้ในการกำหนดความแข็งแรงของวัตถุ มีค่าเท่ากับอัตราส่วนระหว่างความเค้น (stress) และความเครียด (strain)

 

          โมดูลัสของยัง (Young’s Modulus : Y)

          โมดูลัสของยังเป็นปริมาณที่ใช้บอกความเหนียวและความแข็งแรงและทนทานของวัตถุที่มีรูปร่างและองค์ประกอบต่าง ๆ กัน  เมื่อ

                                    =      

          เมื่อ      คือโมดูลัสของยังของวัตถุ มีหน่วยเป็น  หรือ (Pascals)

                   ความเค้น (stress) คืออัตราส่วนระหว่างแรง กับพื้นที่ ที่แรงกระทำ                                       

                   ความเครียด (stain) คืออัตราส่วนระหว่างความยาวที่เปลี่ยนไป  ต่อ                                 ความยาวเดิม    

          ดังนั้นสามารถเขียนใหม่ได้เป็น

                                    =             

                                      =      

                                      =      

          ค่าโมดูลัสของยังของวัตถุแต่ละชนิด จะมีค่าคงที่เสมอภายในขอบเขตยืดหยุ่น ดังนั้นจึงกล่าวได้ว่าภายในขอบเขตยืดหยุ่นความเค้นเป็นปฎิภาคโดยตรงกับความเครียด

 

          ความทนทานต่อแรงอัดและแรงดึงของกระดูก

          (Compressive and Tensile Strength of Bone)

          ความทนทานของต่อแรงดึงและแรงอัด ของวัตถุขึ้นอยู่กับรูปร่างและองค์ประกอบของวัตถุ วัตถุถ้าทนแรงดึงได้ดีไม่จำเป็นต้องทนแรงอัดได้ดี  ถ้าวัตถุชิ้นนั้นคือกระดูก เนื่องจากกระดูกประกอบด้วยส่วนที่เรียกว่า compact และ trabecular  ซึ่งมีองค์ประกอบที่แตกต่างกันมาก  ดังนั้นจึงทำให้ค่าโมดูลัสของยังแตกต่างกันมากด้วย  แสดงดังตารางที่ 1

 

ตารางที่ 1 แสดงค่าความทนทานต่อแรงดึงและแรงอัด และโมดูลัสของยัง ของกระดูก

                Compact และ Trabecular

 

Type of Bone	Compressive Breaking Stress	Tensile Breaking	Young’s Modulus
Compact	170	120	179
Trabecular	2.2	-	0.76

 

 

 

 

 

 

 

 

 

 

 

 

              

 

 

 

 

 

 

 

 

 

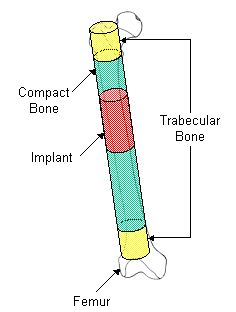
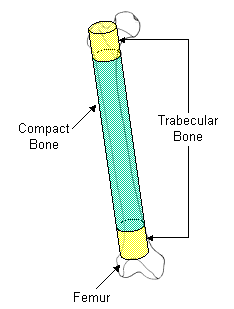
                           ก.                                                        ข.

 

                   รูปที่ 2 แผนภาพแสดงองค์ประกอบของกระดูกเมื่อใช้คำนวณ

 

          รูปที่ 2 แสดงโครงสร้างตามอุดมคติของกระดูกเพื่อใช้ในการคำนวณ  โดยที่กระดูก trabucular จะอยู่ภายในที่จุดกึ่งกลางแล้วกระจายมาถึงส่วนปลายของกระดูก  คล้ายกับค่าที่ได้ในตัวอย่างจะไม่แน่นอน เนื่องจากเป็นการประมาณและความแตกต่างของกระดูกซึ่งแยกกันอย่างชัดเจน

 

ตัวอย่าง  ชายคนหนึ่งมวล  ยืนบนขาข้างเดียว ถ้าขาส่วนล่างและเท้ามีมวลรวมกัน  โดยมีกระดูก femur ยาว  และสมมติให้มีรูปร่างเป็นทรงกระบอกรัศมี  ไม่คิดมวลกระดูก femur

 

 

 

 

 

 

 

 

 

 

 

 

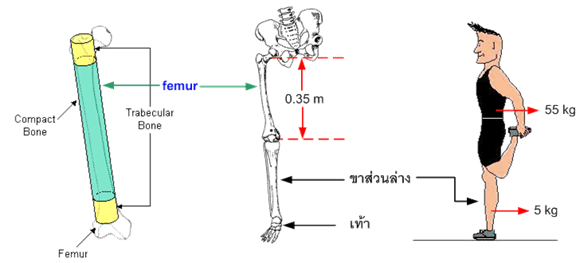
รูปที่ 3

 

 

ก.     จากรูปที่ 3  femur ประกอบด้วยกระดูก compact  และ trabecular  โดยที่  trabecular ที่ปลายแต่ละข้างยาว  กระดูก femur จะหดสั้นลงทั้งหมดเท่าใดเมื่อชายคนนี้ยืนด้วยขาข้างเดียว

ข.     จากรูปที่ 2ข. femur จากข้อ ก. ได้รับการซ่อมแซมด้วยการฝัง polyethylene ซึ่งเป็นสารประกอบอนินทรีย์เพื่อเพิ่มความเกร็ง ยาว   กำหนดให้โมดูลัสของยังของวัสดุที่ใช้มีค่า  กระดูก femur จะหดสั้นลงทั้งหมดเท่าใดเมื่อชายคนนี้ยืนด้วยขาข้างเดียว

วิธีทำ

          ก. เนื่องจาก femur ประกอบด้วยกระดูกสองส่วนซึ่งมีความแตกต่างกัน ดังนั้นในการคำนวณให้แยกพิจารณาที่ละส่วนก่อน  แล้วจึงนำมารวมกันภายหลัง

 

                                    =      

คิดที่ Compact  Bone

                                  =         =      

                                     

จากตารางค่าโมดูลัสของยังของ Compact  Bone มีค่า

 

                                  =    

                                      =      

                                      =      

                                      =      

                                     

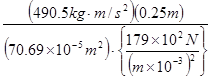
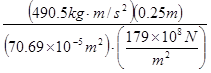
คิดที่ Trabecular  Bone

                                  =         =      

                                     

จากตารางค่าโมดูลัสของยังของ Trabecular  Bone มีค่า

                            

                                  =      

                                      =      

                                      =      

                                      =      

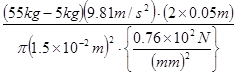
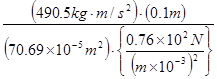
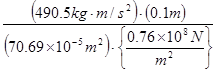
ดังนั้นกระดูก femur จะหดสั้นลงทั้งหมด   + =  =

          ข. เมื่อ  femur ได้รับการซ่อมแซมด้วยการด้วยการฝัง polyethylene ยาว   ทำให้กระดูก femur ประกอบด้วย compact  bone ; trabecular bone และ polyethylene โดยจะทำให้ compact  bone มีความยาวลดลง ส่วน trabecular  bone มีความยาวเท่าเดิมไม่มีการเปลี่ยนแปลง

 

คิดที่ Compact  Bone

                        =         =      

                                     

จากตารางค่าโมดูลัสของยังของ Compact  Bone มีค่า

 

                        =    

                         =      

                             =      

                             =      

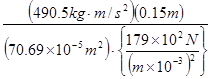
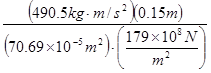
เนื่องจาก trabecular  bone มีความยาวเท่าเดิมไม่มีการเปลี่ยนแปลงใช้ข้อมูลข้อ ก.

คิดที่ polyethylene ซึ่งเป็นสารประกอบอนินทรีย์

                        =         =      

จากโจทย์ค่าโมดูลัสของยังของ  polyethylene  มีค่า  

                        =      

                             =      

                             =      

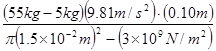
ดังนั้นกระดูก femur จะหดสั้นลงทั้งหมด   +  +  =  =