 |
 |
 |
 |
 |
|
 |
 |
 |
|
|
 |
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 9 การชน
จากบที่ 8 อธิบายเกี่ยวกับโมเมนตัมเชิงเส้นและการอนุรักษ์โมเมนตัมเชิงเส้น โดยไม่กล่าวถึงการชนซึ่งเป็นเงื่อนไขของการเกิดโมเมนตัมเชิงเส้น ในบทนี้จะกล่าวถึงการชนในลักษณะต่าง ๆ
เนื้อหาประกอบด้วย
9.1 ทฤษฎีการดล - โมเมนตัมเชิงเส้น
9.2 การชนแบบยืดหยุ่น
9.3 การชนแบบไม่ยืดหยุ่น
9.1 ทฤษฎีการดล - โมเมนตัมเชิงเส้น
แรงมีผลต่อการเปลี่ยนแปลงโมมเนตัมเชิงเส้นอย่างไร และแรงที่กระทำต่อวัตถุขึ้นอยู่กับอะไร พิจารณาจากกฎข้อสองของนิวตัน
= 
จะได้ 
= 
= 
=
จากสมการที่ได้ค่าทางขวามือเรียกว่า การดล (impulse) แทนการดลด้วย "
" เป็นปริมาณเวกเตอร์จะได้
=
นั่นคือ
=
ดังนั้นทฤษฎีการดล - โมเมนตัมเชิงเส้นคือ
=
ถ้าคุณสังเกตให้ดีจะเห็นความคล้ายคลึงกันระหว่างทฤษฎีการดล - โมเมนตัม กับ
ทฤษฏีงาน - พลังงาน และนิยามของการดล กับนิยามของงาน
|
ทฤษฎีการดล
- โมเมนตัม : |
นิยามการดล
: |
|
ทฤษฎีงาน
- พลังงาน : |
นิยามของงาน
: |
กล่าวคือการเปลี่ยนแปลงพลังงานจลน์ของวัตถุแรงจะขึ้นอยู่กับระยะทาง แต่การเปลี่ยนแปลงโมเมนตัมของวัตถุแรงจะขึ้นกับเวลา
เมื่อปล่อยดินน้ำมันลงบนพื้นแข็งดินน้ำมันจะหยุดนิ่ง
จะได้กราฟแสดงความสัมพันธ์ระหว่างแรง 
กับเวลา 
ขณะชนแสดงดังรูปที่
9.1 (ก) แต่ถ้าปล่อยดินน้ำมันลงบนพื้นที่มีความนุ่ม
จะได้กราฟแสดงความสัมพันธ์ระหว่างแรงกับเวลาขณะชนดังรูปที่ 9.1 (ข)
ก. ข.
รูปที่ 9.1
กรณีทั้งสองที่เกิดขึ้นอัตราการเปลี่ยนแปลงโมเมนตัมจะเท่ากัน จึงทำให้การดลทั้งสองกรณีเท่ากันด้วย โดยอาศัยทฤษฎีการดล - โมเมนตัม ส่วนพื้นที่ใต้กรสฟระหว่างแรงกับเวลาของกราฟทั้งสองคือการดลก็จะมีค่าเท่ากัน เนื่องจากเมื่อดินน้ำมันกระทบพื้นที่มีความนุ่มแรงที่กระทำต่อดินน้ำมันจะน้อยแต่ใช้เวลานาน
อธิบายได้ว่าทำไมเมื่อกระโดดจากที่สูงจึงต้องงอเขา หรือในการรับลูกบอลทำไมต้องเอนตัวและเหวี่ยงแขนไปด้านหลัง เพื่อต้องการให้แรงกระทำมีค่าน้องลงจะช่วยให้เจ็บมือน้อยลง
เมื่อการดลกระทำต่อวัตถุในช่วงเวลาสั้น ๆ แรงกระทำจะสูงมากเช่นการตีลูกเทนนิส รถชนกัน จะทำให้เกิดการบาดเจ็บได้ง่าย
ตัวอย่างที่
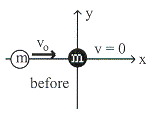
9.1 บอลมวล
เคลื่อนที่ด้วยความเร็ว 
เข้าชนบอลอีกลูกหนึ่งซึ่งมีมวลเท่ากัน
ทำให้บอลลูกแรกหยุดภายในเวลา 
ดังรูปที่ 9.2
จงหา
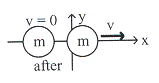
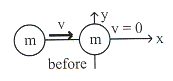
รูปที่ 9.2
ก. การดลของบอลลูกแรก ข. การดลของบอลลูกที่สอง
ค. แรงเฉลี่ยบนบอลลูกแรกขณะชน ง. แรงเฉลี่ยบนบอลลูกที่สองขณะชน
วิธีทำ จากทฤษฎีการดล - โมเมนตัม
ก. 
= = 
= 
= 
= 
ข. = = 
= 
= 
= 
จากนิยามการดล : = 
= 
ค. = 
= 
= 
= 
ง. 
= 
= 
= 
= 
จะสังเกตเห็นว่าแรงทั้งสองมีขนาดเท่ากันแต่ทิศตรงข้ามกัน อธิบายโดยใช้กฎข้อสามของนิวตัน ขณะเดียวกันแรงทีเกิดขึ้นจะมีค่ามากเนื่องจากการชนใช้เวลาสั้น
9.2 การชนแบบยืดหยุ่น
การชนเป็นเหตุการณ์ที่เกิดขึ้นในช่วงเวลาที่สั้นมาก
หมายความว่าแรงภายนอกกระทำในช่วงเวลาสั้น
ๆ เช่นกัน ส่วนการดลของวัตถุเนื่องจากแรงภายนอกสมมติให้มีค่าเป็นศูนย์
อาศัยทฤษฎีการดล - โมเมนตัม
ก็จะทำให้การเปลี่ยนแปลงโมเมนตัมมีค่าเป็นศูนย์เช่นกัน
นั่นคือการอนุรักษ์โมเมนตัม
ถ้าการชนเป็นการอนุรักษ์โมเมนตัม จะอนุรักษ์พลังงานด้วยหรือไม่จากกฎการอนุรักษ์พลังงาน พลังงานที่กล่าวถึงหมายถึงทุกพลังงาน ดังนั้นไม่ควรถามว่าเป็นการอนุรักษ์พลังงาน ควรถามว่าอนุรักษ์พลังงานกลใช่หรือไม่ คำตอบคือการชนแบบยืดหยุ่นจะอนุรักษ์พลังงานจลน์ ส่วนการชนแบบไม่ยืดหยุ่นจะไม่อนุรักษ์พลังงานจลน์
สรุป การชนเป็นการอนุรักษ์โมเมนตัม และพลังงานทั้งหมด ถ้าเป็นการชนแบบยืดหยุ่นจะอนุรักษ์พลังงานจลน์ ถ้าชนแบบไม่ยืดหยุ่นจะไม่อนุรักษ์พลังงานจลน์
ตัวอย่างที่ 9.2 ให้ตรวจสอบกาชนในตัวอย่างที่ 9.1 เป็นการชนแบบยืดหยุ่นหรือไม่
วิธีทำ
 |
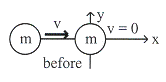
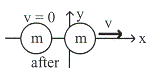จากรูปที่ 9.3
พลังงานจลน์ก่อนชน
= 
= 
พลังงานจลน์หลังชน
= 
=
เป็นการชนแบบยืดหยุ่นเนื่องจากพลังงานจลน์ก่อนชนและหลังชนเท่ากัน
ตัวอย่างที่
9.3 บอลสีขาวเคลื่อนที่ด้วยความเร็ว
ชนแบบยืดหยุ่นกับบอลสีดำซึ่งอยู่นิ่ง
ภายหลังการชนบอลสีขาวเคลื่อนที่เบนไปจากแนวการเคลื่อนที่เดิม 
ส่วนบอลสีดำทำมุม 
กับแนวระดับ ดังรูปที่ 9.4
โดยให้บอลทั้งสองมีมวลเท่ากัน
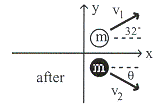
รูปที่ 9.4
วิธีทำ โมเมนตัมเป็นปริมาณเวกเตอร์
ดังนั้นต้องพิจารณาทิศตามแกน โดยมีตัวแปรที่ไม่ทราบค่าสามค่าได้แก่ 
, 
และ ดังนั้นจึงต้องตั้งสามสมการเพื่อใช้ในการแก้ปัญหา
โดยเกิดจากกฎการอนุรักษ์โมเมนตัมสองสมการ คือโมเมนตัมบนแกน 
และแกน 
ส่วนอีกหนึ่งสมการมาจากเงื่อนไขการชนแบบยืดหยุ่นคือการกฎการอนุรักษ์พลังงานจลน์
จากกฎการอนุรักษ์โมเมนตัม
= 
แกน
;
= 
=
= 
(1)
แกน
;
= 
= 
(2)
ชนแบบยืดหยุ่นจะได้ว่า
= 
= 
= 
(3)
(2) / (1) จะได้
= 
=
= 
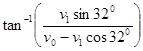(4)
ยกกำลังสองสมการที่ (1) และ (2) แล้วนำมารวมกัน
= 
= 
= 
= 
(5)
แทนค่า
จาก (5) ลงใน
(3)
= 
= 
= 
= 
= 
แทนค่า
ลงใน (3)
=
= 
= 
= 
= 
แทนค่าต่าง ๆ ลงในสมการ (4)
=
= 
= 
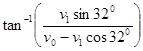
สังเกต
การชนแบบยืดหยุ่นผลรวมของมุมจะเท่ากับ 
9.3 การชนแบบไม่ยืดหยุ่น
การชนแบบไม่ยืดหยุ่นจะอนุรักษ์พลังงาน แต่ในระหว่างการชนจะเกิดความร้อนจึงไม่อนุรักษ์พลังงานจลน์แต่ยังคงอนุรักษ์โมเมนตัม
ตัวอย่างที่
9.4 ตู้รถไฟมวล
วิ่งเข้าชนตู้รถไฟอีกตู้หนึ่งมวล
ซึ่งจอดอยู่นิ่งด้วยความเร็ว 
ทำให้ตู้ทั้งสองเคลื่อนที่ติดไปด้วยกันจงหา
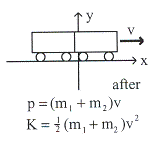
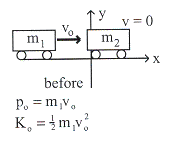
ก. ความเร็วของตู้รถไฟหลังชน
ข. อัตราส่วนพลังงานจลน์ที่สูญเสียระหว่างชน
วิธีทำ ก. จากกฎการอนุรักษ์พลังงาน
= 
= 
= 
= 
= 
ข. อัตราส่วนพลังงานจลน์ที่สูญเสียระหว่างการชน
= 
= 
= 
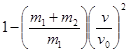
แทนค่าต่าง ๆ ในสมการ
= 
= 
= 
พลังงานสูญเสียงานแสดงว่าพื้นมีแรงเสียดทานมาก แต่พลังงานไม่มีการสูญหาย แต่เปลี่ยนเป็นพลังงานจลน์ทำให้อะตอมและโมเลกุลภายในวัตถุสั่นเกิดเป็นความร้อน
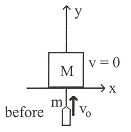ตัวอย่างที่ 9.5 ยิงกระสุนมวล 
ในแนวดิ่งเข้าชนแท่งไม้มวล 
ด้วยความเร็ว 
ทำให้กระสุนฝังอยู่ในแท่งไม้ทำให้แท่งไม้เคลื่อนที่ดังรูปที่
9.5 จงหา
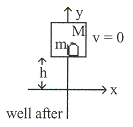
โมเนตัมหายไปไหน
รูปที่ 9.5
วิธีทำ ก. พิจารณากระสุนก่อนชนแท่งไม้และขณะชนแท่งไม้โดยอาศัยกฎการอนุรักษ์โมเมนตัม
= 
= 
= 
(1)
พลังงานก่อนชนและหลังชนจะมีค่าเท่ากัน แต่งานที่เกิดขณะที่ลูกกระสุนฝังเข้าไปในแท่งไม้เป็นงานเนื่องจากแรงไม่อนุรักษ์ ซึ่งจะเปลี่ยนเป็นความร้อน เมื่อจับพลังงานสองส่วนนี้มาเท่ากันก็ไม่สามารถคำนวณหาความสูงได้ แต่อย่างไรก็ตามภายหลังการชน (แท่งไม้ยกตัวขึ้นสูง) จะเกิดแรงอนุรักษ์เนื่องจากแรงโน้มถ่วงกระทำต่อแท่งไม้
จากฎการอนุรักษ์พลังงาน
= 
= 
= 
= 
(2)
แทนค่า
จาก (1) ลงใน (2)
= 
= 
= 
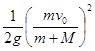
ข. จากฎการอนุรักษ์พลังงาน
=
= 
แทนค่าต่าง ๆ ลงในสมการ
= 
= 
นั่นคือพลังงานส่วนมากจะกลายเป็นความร้อนระหว่างชน
สรุป
นิยามโมเมนตัมเชิงเส้น : 
กฎพื้นฐานข้อสอง
: 
นิยามการดล
: 
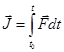
ทฤษฎีการดล
- โมเมนตัม : 
