 |
 |
 |
 |
 |
|
 |
 |
 |
|
|
 |
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 6 พลังงานจลน์และงาน
เนื้อหาประกอบด้วย
6.1 คำจำกัดความของงาน
6.2 ทฤษฎีงาน - พลังงาน
6.3 คำจำกัดความของกำลัง
พิจารณาการตกของวัตถุเกิดจากอะไรผลเป็นย่างไร การตกของวัตถุเกิดจากแรงซึ่งเป็นปริมาณเวกเตอร์ผลทำให้เกิดงานเป็นปริมาณสเกลาร์
6.1 คำจำกัดความของงาน
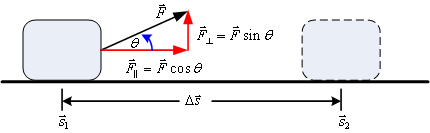
รูปที่ 6.1
จากรูปที่ 6.1 แสดงแรงที่กระทำกับวัตถุซึ่งมีทิศเดียวกับการเคลื่อนที่
ทำให้วัตถุมีความเร่ง ขณะที่แรงกระทำกับวัตถุมีทิศตั้งฉาก
กับการเคลื่อนที่ไม่มีผลต่อความเร่งของวัตถุ
งานที่ได้จะเกิดจากแรงที่มีทิศเดียวกับการเคลื่อนที่เท่านั้น
หรือกล่าวได้ว่าแรงกับการกระจัดจะต้องมีทิศทางแนวเดียวกัน
งานเนื่องจากแรงคงที่
งานที่เกิดจากแรงคงที่ คือผลคูณระหว่างแรงกับการกระจัดซึ่งมีทิศเดียวกัน
= 
หรือ 
= 
= 
หน่วยของงาน 
= 
= 
หน่วยที่ใช้เรียกงานโดยเฉพาะคือ จูล โดยที่ 
เป็นปริมาณสเกลาร์
ตัวอย่างที่
6.1 ออกแรง
กระทำต่อกระเป๋าเดินทางขนาด 
โดยทำมุม 
กับแนวระดับดังรูปที่ 6.2 ทำให้กระเป๋าเดินทางเคลื่อนที่ด้วยความเร็วคงที่บนผิวขรุขระได้ระยะทาง 
จงคำนวณหางานที่เกิดจากแรงต่าง ๆ
ที่กระทำต่อกระเป๋าเดินทาง
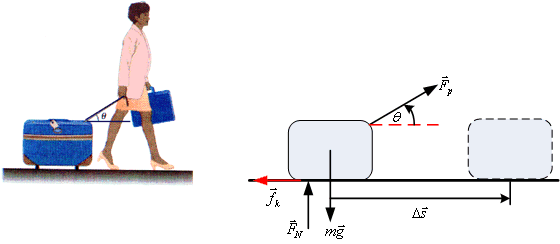
รูปที่ 6.2
วิธีทำ คำนวณหาขนาดของแรงต่าง ๆ ที่กระทำต่อกระเป๋าเดินทาง จากกฎข้อที่สองของนิวตัน พิจารณาแนวแรงตามรูปที่ 6.3
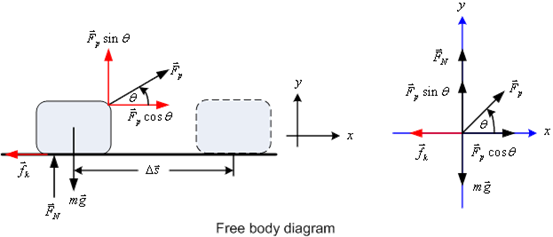
รูปที่ 6.3
= 
= 
= 
= 
=
= 
ดังนั้นแรงต่าง ๆ ที่กระทำต่อกระเป๋าเดินทางคือ
= 
= 
= 
= 
= 
=
= 
= 
= 
จากคำจำกัดความของงาน
= 
= 
= 
= 
เป็นงานที่เกิดจากแรงซึ่งมีทิศเดียวกับการกระจัดซึ่งมีเพียงแรงเดียวเท่านั้น
=
= 
= 
= 
= 
เป็นงานที่เกิดจากแรงเสียดทานซึ่งมีทิศตรงกันข้ามกับการกระจัด
ดังนั้นเมื่อแตกแรง เข้าการกระจัดคือ 
จึงมีค่าเป็นลบ
=
= 
= 
= 
=
ไม่เกิดงานเนื่องจากแรงทั้งสอง เนื่องจากแรงทั้งสองไม่ทำให้เกิดการกระจัดในทิศเดียวกับแรงทั้งสอง
งานสุทธิที่กระทำต่อกระเป๋าเดินทางคืองานรวมทั้งหมดซึ่งมีค่าเท่ากับศูนย์เนื่องจากกระเป๋าไม่มีความเร่งนั่นคือ
= 
= 
=
พิจารณากรณีกระเป๋าเดินทางมีความเร่งดังตัวอย่างต่อไปนี้
ตัวอย่างที่
6.2 จากตัวอย่างที่
6.1 ถ้าพื้นมีสัมประสิทธ์ความเสียดทานจลน์ 
วิธีทำ ตัวอย่างที่ 6.1 และ 6.2 แตกต่างกันเพียงเล็กน้อยเท่านั้นโดยที่ในตัวอย่างที่ 6.2 พื้นจะมีสัมประสิทธ์ความเสียดทานจลน์เข้ามาเกี่ยวข้องอาศัยรูปที่ 6.2 และ 6.3 และข้อมูลจากตัวอย่างที่ 6.1
จาก 
= 
= 
= 
= 
งานที่กระทำโดยแรงเสียดทานคือ
=
=
=
= 
= 
ส่วนงานที่เกิดจากแรงต่างๆ จะมีค่าเท่ากับงานที่เกิดจากแรงในตัวอย่างที่ 6.1 นั่นคือ
=
; 
; 
ดังนั้นงานสุทธ์ที่กระทำต่อกระเป๋าเดินทางคือ
=
= 
= 
เป็นงานสุทธิซึ่งเกิดจากแรงต่าง ๆ ที่กระทำต่อกระเป๋าเดินทางทำให้กระเป๋าเดินทางเคลื่อนที่ด้วยความเร่ง
จากคำจำกัดความของงานเมื่อเขียนอยู่ในรูปสมการ
ดังรูปที่ 6.4 ทำให้ยุ่งยากและไม่สะดวกในการคำนวณ เพื่อให้ง่ายในการแก้สมการสามารถเขียนได้ใหม่โดยใช้ผลคูณแบบดอต
(dot product)
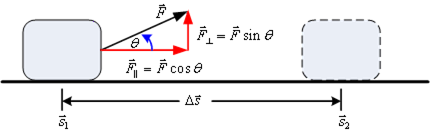
รูปที่ 6.4
= 
เมื่อนำมาเปรียบเทียบกับสมการอันเดิมจะเหมือนกันคือ
=
= 
=
งานเนื่องจากแรงไม่คงที่
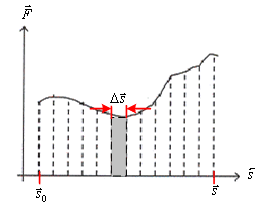
เมื่อแรง 
แปรตามระยะทาง
ทำให้วัตถุเคลื่อนที่ดังกราฟรูปที่
6.5 การคำนวณหางานที่เกิดขึ้น
สามารถทำได้เช่นเดียวกับงานที่เกิดจากแรงคงที่ โดยการแบ่งระยะทางระหว่าง 
ถึง เป็นส่วนเล็ก ๆ คือ 
ซึ่งแต่ละส่วนเล็ก ๆ
มีค่าเกือบคงที่ และส่วนเล็ก ๆ นี้จะทำให้เกิดงานย่อย ๆ
ดังนั้นงานที่เกิดขึ้นทั้งหมดคือ
รูปที่ 6.5
ผลรวมของงานย่อย ๆ ที่เกิดขึ้น
= 
= 
เมื่อระยะทางมีขนาดเล็กมาก ๆ อย่างต่อเนื่อง
ดังนั้นงานทั้งหมดคือพื้นที่ใต้กราฟซึ่งหาได้โดยการอินทิเกรต 
จาก ถึง เนื่องจาก มีค่าน้อยมาก ๆ ดังนั้นสามารถเขียนแทนได้เป็น
=
= 
= 
=
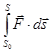
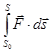
ดังนั้นงานที่เกิดจากแรงไม่คงที่คือ
= 
เช่นงานที่ใช้ในการดึงหรือกดสปริง
ตัวอย่างที่
6.3
ออกแรงดึงสปริงในแนวราบทำให้สปริงยืดออกเป็นระยะทาง
ดังรูปที่ 6.6 จงหางานที่กระทำโดยสปริง
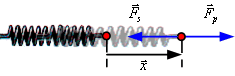วิธีทำ เมื่อออกแรง 
ดึงสปริง สปริงจะออกแรงดึงกลับ 
ซึ่งมีขนาดเท่ากันแต่ทิศทางตรงกันข้าม
โดยแรงดึงกลับจะเป็นปฏิภาคโดยตรงกับ เมื่อ คือระยะยืดหรือหดจากจุดสมดุล
รูปที่ 6.6 
= 
เมื่อ 
คือค่าคงตัวของสปริง (spring
constant) เรียกว่าค่านิจสปริง
ถ้าออกแรงดึงที่ปลายสปริงให้ยืดออกเป็นระยะทาง จากกฎข้อสองของนิวตันจะได้ว่า
= 
=
= = 
งานที่ใช้ในการดึงสปริงคือ
=
= 
= 
= 
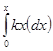
6.2 ทฤษฎีงาน - พลังงาน
จากหัวข้อที่แล้วพิจารณางานสุทธิที่กระทำต่อวัตถุ แล้วทำให้วัตถุมีความเร่ง พิจารณาจากคำจำกัดความของงานและอาศัยกฎข้อที่สองของนิวตันจะได้ว่า
=
= 
= 
=
จากคำจำกัดความของความเร่งและความเร็ว
= 
= 
= 
= 
สมมุติให้วัตถุมีความเร็วต้น
และความเร็วปลาย 
= 
= 
=
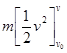
นั่นคืองานสุทธิที่กระทำต่อวัตถุ
จะทำให้วัตถุมีการเปลี่ยนแปลงปริมาณปริมาณหนึ่ง เมื่อ 
เรียกว่าพลังงานจลน์
พลังงานจลน์
=
ดังนั้นงานสุทธิที่กระทำต่อวัตถุสามารถเขียนใหม่ได้เป็น
= 
สมการนี้เรียกว่าทฤษฎีของงาน –
พลังงาน
ทฤษฎีงาน - พลังงาน
= 
สรุป ได้ว่างานสุทธิที่กระทำต่อวัตถุจะทำให้วัตถุเกิดการเปลี่ยนแปลงพลังงานจลน์
ตัวอย่างที่
6.4 ปล่อยทรงกลมจากความสูง
ดังรูปที่ 6.7 จงคำนวณหาความเร็วขณะกระทบพื้น
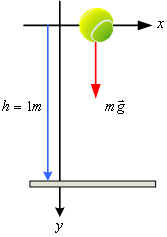วิธีทำ เนื่องจากเป็นการเคลื่อนที่แบบดิ่งอิสระสามารถคำนวณโดยใช้สมการการเคลื่อนที่จากบทที่แล้วก็ได้
ทดสอบโดยการแปลงค่าจากทฤษฎีงาน - พลังงาน เมื่องานสุทธิที่ได้เกิดจากแรงโน้มถ่วง
จากคำจำกัดความของงาน
=
= 
= 
= 
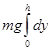
รูปที่ 6.7
จากทฤษฎีงาน - พลังงาน เมื่อมีการกระทำต่อวัตถุจะทำให้พลังงานจลน์ของวัตถุเปลี่ยนแปลง
=
= 
= 
= 
แต่
ดังนั้น = 
(เปรียบเทียบสมการนี้กับสมการที่ได้จากตัวอย่างที่ 6.7 )
จะได้
= 
= 
= 
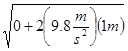
หมายเหตุ ปัญหาที่เกิดจากการชนไม่สามารถแก้โดยใช้พลังงานจลน์ได้
ตัวอย่างที่
6.5 นำมวล
อัดสปริงซึ่งมีค่านิจสปริงเท่ากับ 
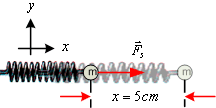
ทำให้สปริงหดเข้าไปเป็นระยะทาง 
ดังรูปแล้วปล่อย จงหา
ก. งานที่สปริงกระทำกับมวล 
ข. พลังงานจลน์และความเร็วของมวล ขณะที่ออกจาก สปริง
วิธีทำ ก. =
= 
= 
=
= 
= 
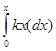
ข. =
=
= 
=
แต่ =
= 
= 
= 
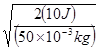
จากตัวอย่างนี้แสดงให้เห็นว่างานสุทธิ์เป็นผลทำให้เกิดพลังงานจลน์
โจทย์ข้อนี้สามารถคำนวณได้อีกวิธีหนึ่งคือใช้กฎข้อสองของนิวตัน แล้วใช้คำจำกัดความของความเร่งจากนั้นอินทิเกรตหาความเร็วซึ่งมีความยุ่งยาก ดังนั้นเพื่อความสะดวกจึงใช้ทฤษฎีงาน - พลังงาน
คำนวณโดยใช้กฎของนิวตันจาก
=
= 
= 
= 
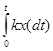แต่
=
= 
= 
= 
=
= 
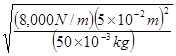
6.3 คำจำกัดความของกำลัง
กำลังคือ : อัตราการทำงาน
เขียนอยู่ในรูปสมการทางคณิตศาสตร์ได้ดังนี้
คำจำกัดความของกำลัง
= 
= 
= 
หน่วยของกำลังเป็น 
หรือวัตต์ (Watt) เขียนย่อ
นอกจากนี้หน่วยของกำลังยังเรียกอีกอย่างหนึ่งว่ากำลังม้า
(horse
power) เขียนย่อเป็น 
บางครั้งเขียนหน่วยของพลังงาน
(หรืองาน) ในพจน์ของกำลังเป็น กิโลวัตต์ - ชั่วโมง 
ซึ่งเป็นพลังงานที่เปลี่ยนรูปหรือสิ้นเปลืองนับเป็นกิโลวัตต์ในเวลา
1 ชั่วโมงโดย
= 
= 
เช่นหลอดไฟ 
จะใช้พลังงาน 
ตัวอย่างที่ 6.6 รถยนต์คันหนึ่งเครื่องยนต์มีกำลัง
วิ่งด้วยความเร็ว 
ภายในเวลา 
จงหา
ก. งานที่ทำโดยเครื่องยนต์
ข. แรงเสียดทานของรถยนต์
วิธีทำ ก. =
= 
= 
= 
= 
= 
= 
= 
ข. จาก = = 
= 
=
= 
= 
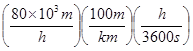
เมื่อรถวิ่งด้วยความเร็วคงที่ แรงสุทธิ์ที่กระทำต่อรถจะมีค่าเป็นศูนย์ นั่นคือแรงเสียดทานที่กระทำกับรถยนต์จะมีค่าเท่ากับแรงที่เครื่องยนต์จ่ายออกมาแต่ทิศทางตรงกันข้าม ดังนั้นกำลังที่จ่ายออกมาบางส่วนจะสูญเสียให้แก่แรงเสียดทาน
จาก = 
=
= 
= 
= 
สรุป
คำจำกัดความของงาน :
=
คำจำกัดความของพลังงานจลน์
: =
ทฤษฎีงาน - พลังงาน
: =
คำจำกัดความของกำลัง : =
