 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 7 พลังงานศักย์ และการอนุรักษ์พลังงาน
เมื่อลูกบอลกลิ้งขึ้นพื้นเอียง สามารถอธิบายการหยุดของลูกบอลได้โดยอาศัยทฤษฎีงาน - พลังงาน แต่พลังงานเกิดได้อย่างได้และอยู่ที่ไหน ในทำนองเดียวกันเมื่ออกแรงผลักกล่องบนพื้นราบทฤษฎีงาน - พลังงาน สามารถใช้อธิบายการหยุดของกล่องได้ แต่พลังงานเกิดได้อย่างได้และอยู่ที่ไหน คำถามเหล่านี้มีคำตอบเมื่อนักศึกษาได้ศึกษาในบทนี้
กฎการอนุรักษ์พลังงาน
พลังงานสามารเปลี่ยนรูปจากรูปแบบหนึ่งไปยังอีกรูปแบบหนึ่งได้ แต่ผลรวมของพลังงานยังคงที่ กฎการอนุรักษ์พลังงานมีความสำคัญมากเนื่องจากมีประโยชน์ที่สามารถใช้อธิบายหรือตอบคำถามต่าง ๆ ได้ ไม่เฉพาะในทางฟิสิกส์เท่านั้น ในสาขาต่าง ๆ ทางวิทยาศาสตร์ก็สามารถนำไปใช้อธิบายได้
เนื้อหาประกอบด้วย
7.1 แรงอนุรักษ์และแรงไม่อนุรักษ์
7.2 งานและพลังงานศักย์
7.3 ชนิดของพลังงานศักย์
7.4 กฎการอนุรักษ์พลังงาน
7.1 แรงอนุรักษ์และแรงไม่อนุรักษ์
ทำไมแรงโน้มถ่วงกลายเป็นพลังงานได้ ส่วนแรงเสียดทานทำไม่ได้ เราสามารถใช้วิชาฟิสิกส์ตอบคำถามเหล่านี้ได้ กล่าวคืองานที่กระทำโดยแรงโน้มถ่วงเกิดขึ้นระหว่างจุด 2 จุด ซึ่งเป็นอิสระต่อกัน (ไปตามเส้นทางไหนก็ได้) แต่งานเนื่องจากแรงเสียดทานไม่เป็นเช่นนั้น
ตัวอย่างที่
7.1 บอลมวล
![]() กลิ้งจากฐานพื้นเอียงจนถึงขอบบนสุดของพื้นเอียงซึ่งสูงจากพื้น
กลิ้งจากฐานพื้นเอียงจนถึงขอบบนสุดของพื้นเอียงซึ่งสูงจากพื้น
![]() ดังรูปที่ 7.1 จงหางานที่กระทำโดยแรงโน้มถ่วงตามเส้นทางต่อไปนี้
ดังรูปที่ 7.1 จงหางานที่กระทำโดยแรงโน้มถ่วงตามเส้นทางต่อไปนี้
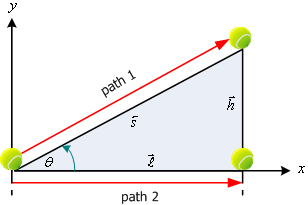
ก. ตามพื้นเอียง (path 1)
ข. ตามแนวราบ (path 2)
รูปที่ 7.1
วิธีทำ ก. ตามพื้นเอียง (path 1)
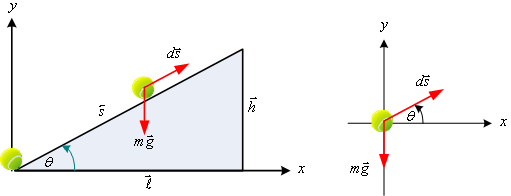
รูปที่ 7.2
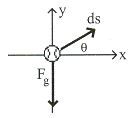
![]() =
= ![]()
![]() =
= ![]()
จากรูปที่
7.2 มุมระหว่าง ![]() กับ
กับ ![]() มีค่าเท่ากับ
มีค่าเท่ากับ ![]() จะได้
จะได้
![]() =
= ![]()
แต่
![]()
![]() =
= ![]()
แต่ ![]() ,
, ![]() และ
และ ![]() เป็นค่าคงที่
เป็นค่าคงที่
![]() =
= ![]()
= ![]()
แต่ ![]() จะได้
จะได้
![]() =
= ![]()
= ![]()
= ![]()
ข. งานตามแนวราบ (part 2)
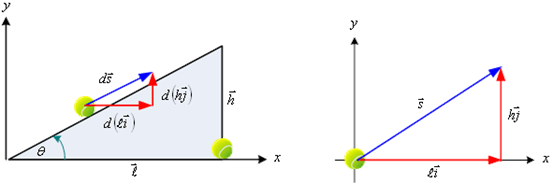
เนื่องจากวัตถุเคลื่อนที่ตามพื้นเอียง ![]() ดังนั้นเมื่อแยกองค์ประกอบจะได้
ดังนั้นเมื่อแยกองค์ประกอบจะได้ ![]() (กลิ้งขึ้นพื้นเอียง)
(กลิ้งขึ้นพื้นเอียง)
![]() =
= ![]()
![]() =
= ![]()
แต่
![]() ;
; ![]()
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
จากข้อ ก. และ ข. จะสังเกตุได้ว่างานเนื่องจากแรงโน้มถ่วงไม่ขึ้นกับแนวทางการเคลื่อนที่ ขึ้นอยู่กับจุดเริ่มต้นและจุดสุดท้ายเท่านั้น
ตัวอย่างที่
7.2 กล่องมวล
![]() เคลื่อนที่ตามพื้นเอียงจากจุด
เคลื่อนที่ตามพื้นเอียงจากจุด![]() ถึงจุด
ถึงจุด ![]() จงหางานเนื่องจากแรงเสียดทานตามเส้นทางที่
1 (path 1) และเส้นทางที่ 2 (path2) ดังรูปที่
7.3 กำหนดให้สัมประสิทธ์แรงเสียดทานเท่ากับ
จงหางานเนื่องจากแรงเสียดทานตามเส้นทางที่
1 (path 1) และเส้นทางที่ 2 (path2) ดังรูปที่
7.3 กำหนดให้สัมประสิทธ์แรงเสียดทานเท่ากับ ![]()
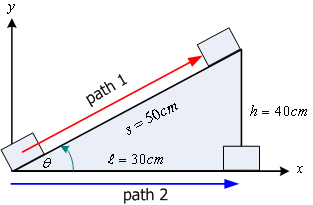
รูปที่ 7.3
วิธีทำ จากกฎข้อสองของนิวตัน
และแรงปฎิกริยาในแนวตั้งฉาก ![]() จะมีค่าเท่ากับน้ำหนักของวัตถุ
จะมีค่าเท่ากับน้ำหนักของวัตถุ
![]() แต่จากสมการ
แต่จากสมการ
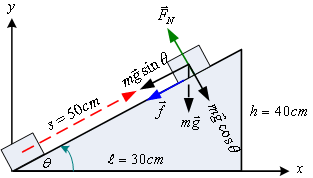
![]() =
= ![]()
![]() =
= ![]()
= ![]()
จากคำจำกัดความของงาน แรงเสียดทานจะมีทิศตรงข้ามกับการเคลื่อนที่จะได้
![]() =
= ![]()
![]() =
= ![]()
คิดตามเส้นทางที่ 1 (part 1)
![]() =
= ![]()
พิจารณาทิศตามพื้นเอียง
จะได้ว่าแรง ![]() มีทิศตรงข้ามกับการเคลื่อนที่
มีทิศตรงข้ามกับการเคลื่อนที่ ![]()
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
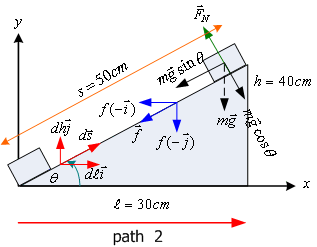 คิดตามเส้นทางที่
2
(part 2)
คิดตามเส้นทางที่
2
(part 2)
![]() =
= ![]()
แต่แรง ![]() จะมีทิศตรงข้ามกับการเคลื่อนที่ ดังนั้น
จะมีทิศตรงข้ามกับการเคลื่อนที่ ดังนั้น
![]() และ
และ![]()
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
งานที่เกิดจาดแรงเสียดทานจะขึ้นกับแนวทางการเคลื่อนที่
งานที่ไม่ขึ้นกับแนวทางการเคลื่อนที่ จะถูกเก็บไว้ในรูปของพลังงาน และจะเกิดการสะสมพลังงาน เป็นแรงอนุรักษ์
งานที่ขึ้นกับแนวทางการเคลื่อนที่ จะสูญเสียพลังงาน เป็นแรงไม่อนุรักษ์
7.2 งานและพลังงานศักย์
พิจารณาลูกบอลเคลื่อนที่ขึ้นตามพื้นเอียงดังรูปที่ 7.4
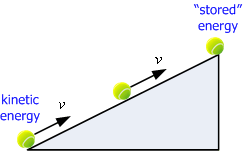
ถ้าใช้กฎการอนุรักษ์พลังงาน จะได้ว่าพลังงานจะเก็บสะสมอยู่ที่ปลายบนสุดของพื้นเอียง ซึ่งจะมีค่าเท่ากับพลังงานจลน์ที่อยู่ปลายล่างสุดของพื้นเอียง
พลังงานที่เก็บสะสมอยู่ที่ปลายบนสุดของพื้นเอียงเรียกว่า " พลังงานศักย์ "
จากรูปที่ 7.4 พลังงานทั้งหมดของระบบเป็นพลังงานจลน์
![]() เมื่อลูกบอลเคลื่อนที่ขึ้นตามพื้นเอียงพลังงานศักย์
เมื่อลูกบอลเคลื่อนที่ขึ้นตามพื้นเอียงพลังงานศักย์
![]() ก็
ก็
รูปที่ 7.4 จะเพิ่มขึ้น พลังงานจลน์ก็จะน้อยลง ตามกฎ
การอนุรักษ์พลังงาน กล่าวคือพลังงานของทั้งระบบจะคงที่ไม่เปลี่ยนแปลง
![]()
พิจารณาลูกบอลเคลื่อนที่ขึ้นตามพื้นอียงดังรูปที่ 7.5 ก. และ 7.5 ข.
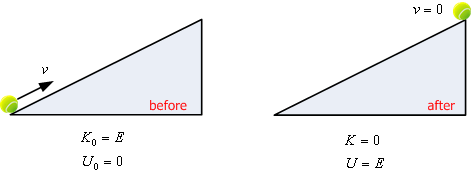
รูปที่ 7.5 ก. รูปที่ 7.5 ข.
จากรูปที่ 7.5 ก. และ 7.5 ข. จะได้ว่า
รูปที่ 7.5 ก. ![]()
รูปที่ 7.5 ข. ![]()
นั่นคือพลังงานจลน์สามารถเปลี่ยนเป็นพลังงานศักย์ได้ ตามทฤษฎีของงาน - พลังงาน
![]() =
= ![]()
โดยทั่ว ๆ ไปงานเกิดได้ทั้งจากแรงอนุรักษ์และแรงไม่อนุรักษ์ แต่แรงอนุรักษ์เท่านั้นที่เกี่ยวข้องกับพลังงานศักย์ ในกรณีเราสมมุติให้ไม่มีแรงภายนอก(แรงไม่อนุรักษ์) มากระทำจะได้
![]() =
= ![]()
![]() =
= ![]()
จากกฎการอนุรักษ์พลังงาน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
พลังงานศักย์เท่านั้นที่มีความสัมพันธ์กับแรงอนุรักษ์ ดังนั้นนิยามของพลังงานศักย์คือ
![]() =
= ![]()
ตัวอย่างที่ 7.3 จงหา ก. พลังงานศักย์ของลูกบอลที่จุดบนสุดของพื้นเอียง
ข. ความเร็วที่ปลายล่างของพื้นเอียง
วิธีทำ ก.
จากตัวอย่างที่ 7.1 ![]() และจากนิยามของพลังงานศักย์
และจากนิยามของพลังงานศักย์
![]() =
= ![]()
= ![]()
![]() =
= ![]()
การเปลี่ยนแปลงที่สังเกตุได้ชัดเจนคือพลังงานศักย์ ซึ่งขึ้นอยู่กับตำแหน่งอ้างอิงที่เรากำหนด โดยกำหนดให้จุดเริ่มต้นหรือจุดสุดท้ายมีพลังงานศักย์เป็นศูนย์ก็ได้ ในที่นี้กำหนดให้จุดเริ่มต้นคือที่ปลายพื้นเอียงมีพลังงานศักย์เป็นศูนย์ ดังนั้น
![]() =
= ![]()
ข. ความเร็วที่ปลายพื้นเอียงสามารถหาได้โดยใช้กฎการอนุรักษ์พลังงาน
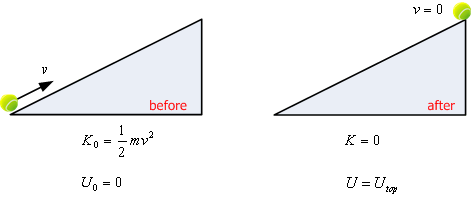
จากสมการ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าในสมการ
![]() =
= ![]()
= ![]()
การแก้ปัญหาโดยใช้กฎการอนุรักษ์พลัลงานจะทำได้ง่ายกว่าการใช้แรง และกฎข้อสองของนิวตันในการคำนวณหาความเร่งได้ง่ายสะดวกกว่าใช้สมการจลศาสตร์
ใจความสำคัญในบทนี้
ทฤษฎีงาน - พลังงาน ![]()
นิยามของพลังงานศักย์ ![]()
กฎการอนุรักษ์พลังงาน ![]() (อนุรักษ์แรงเท่านั้น)
(อนุรักษ์แรงเท่านั้น)
7.3 ชนิดของพลังงานศักย์
พลังงานศักย์เป็นแรงอนุรักษ์ พิจารณาความแรงโน้มถ่วงและสปริง
พลังงานศักย์โน้มถ่วง
พิจารณาลูกบอลดังรูปที่ 7.6 จากนิยามของงานและพลังงานจะได้ว่า
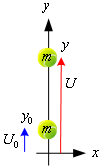
![]() =
= ![]()
![]() =
= ![]()
= 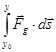
พิจารณารูปที่ 7.6 ในระบบแกนมุมฉากระยะทางในแกน ![]() จะมีค่าเพิ่มในทิศขึ้น
แต่ในกรณีนี้น้ำหนักและการกระจัดจะมีทิศตรงกันข้ามเมื่อ
จะมีค่าเพิ่มในทิศขึ้น
แต่ในกรณีนี้น้ำหนักและการกระจัดจะมีทิศตรงกันข้ามเมื่อ ![]() จะได้
จะได้
รูปที่ 7.6
![]() =
= 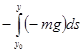
= 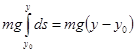
![]() =
= ![]()
จะได้ความสัมพันธ์ของพลังงานศักย์โน้ม่วงดังนี้
พลังงานศักย์โน้มถ่วง ![]() =
= ![]() เมื่อ
เมื่อ ![]()
ตัวอย่างที่ 7.4 ฟักทองตกจากที่สูง 62 m สู่พื้นดินดังรูปที่ 7.7 จงหาความเร็วขณะกระทบพื้น
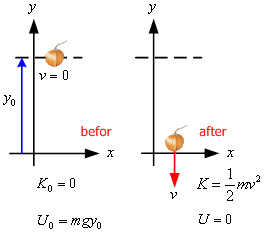
รูปที่ 7.7
วิธีทำ โจทย์ข้อนี้สามารถคำนวณได้โดยใช้การเปลี่ยนพลังงานศักย์เป็นพลังงานจลน์
จากนั้นใช้กฎการอนุรักษ์พลังงาน โดยเลือกพื้นเป็นจุดอ้างอิงที่จุดนี้ ![]() ดังนั้นพลังงานศักย์จึงเป็รนศูนย์ด้วย
ดังนั้นพลังงานศักย์จึงเป็รนศูนย์ด้วย
![]() =
= ![]() =
= ![]()
![]() =
= ![]() =
= ![]()
จากกฎการอนุรักษ์พลังงาน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
ซึ่งเหมือนกับการเคลื่อนที่แบบดิ่งอิสระเปรียบเทียบกับตัวอย่างที่ 6.4 แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
พลังงานศักย์สปริง
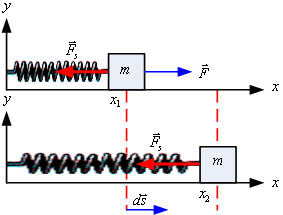
รูปที่ 7.8
จากนิยามของพลังงานศักย์พิจารณามวลติดปลายสปริงดังรูปที่
7.8 เดิมมวล ![]() วางอยู่ที่ตำแหน่ง
วางอยู่ที่ตำแหน่ง ![]() เมื่อเคลื่อนมวลไปทางขวามือมาอยู่ที่ตำแหน่ง
เมื่อเคลื่อนมวลไปทางขวามือมาอยู่ที่ตำแหน่ง
![]() จากนั้นใช้คำจำกัดของงาน
จากนั้นใช้คำจำกัดของงาน
![]() =
= ![]()
![]() =
= ![]() =
= 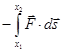
แรงที่สปริงกระทำต่อมวลจะมีทิศตรงข้ามกับการกระจัดจะได้
![]() =
= 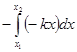
= ![]()
= ![]()
![]() =
= ![]()
จะได้ความสัมพันธ์ของพลังงานศักย์สปริงคือ
พลังงานศักย์สปริง ![]() เมื่อ
เมื่อ ![]() คือระยะยืดหรืดหดจากตำแหน่งสมดุล
คือระยะยืดหรืดหดจากตำแหน่งสมดุล
ตัวอย่างที่ 7.5 วางมวล
![]() บนสปริงซึ่งอยู่ในตำแหน่งสมดุลทำให้สปริงหดเป็นระยะ
บนสปริงซึ่งอยู่ในตำแหน่งสมดุลทำให้สปริงหดเป็นระยะ
![]() ดังรูปที่ 7.9 จงหาค่าคงที่ของสปริง
ดังรูปที่ 7.9 จงหาค่าคงที่ของสปริง
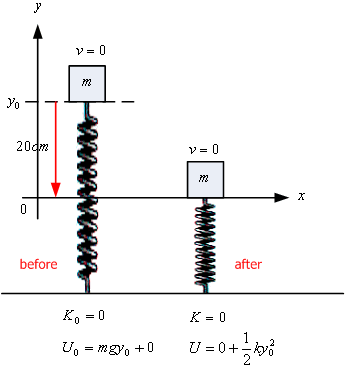
รูปที่ 7.9
วิธีทำ จากระบบพิกัดฉากเลือกตำแหน่งที่สปริงหดตัวเป็นจุดอ้างอิง
![]() ดังนั้นการเปลี่ยนแปลงพลังงานจลน์และพลังงานศักย์สามารถหาได้ดังนี้
ดังนั้นการเปลี่ยนแปลงพลังงานจลน์และพลังงานศักย์สามารถหาได้ดังนี้
![]() =
= ![]() =
= ![]()
![]() =
= ![]()
จากกฎการอนุรักษ์พลังงาน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าในสมการ
![]() =
= ![]()
= ![]()
การแก้ปัญหาโดยใช้พลังงานจะง่ายกว่าการคำนวณโดยารใช้แรง
7.4 กฎการอนุรักษ์พลังงาน
กฎการอนุรักษ์พลังงาน : พลังงานสามารถเปลี่ยนจากรูปหนึ่งไปยังอีกรูปหนึ่งได้ โดยที่ผลรวมของพลังงานทั้งหมดจะคงที่
จากทฤษฎีของงานและพลังงานหัวข้อที่ 6.2
![]() =
= ![]()
จากนิยามของพลังงานศักย์
![]() =
= ![]()
งานสุทธิ
![]() =
= ![]()
แทนค่างานสุทธ์ลงในทฤษฎีงานและพลังงาน และใช้นิยามของพลังงานศักย์จะได้ว่า
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อแสดงเป็นสมการทางคณิตศาสตร์กฎการอนุรักษ์พลังงาน ประกอบด้วยแรงไม่อนุรักษ์
กฎการอนุรักษ์พลังงาน ![]() =
= ![]()
ตัวอย่างที่ 7.6 ฟักทองมวล
![]() จากตัวอย่างที่ 7.4 ในความเป็นจริงขณะกระทบพื้นมีความเร็ว
จากตัวอย่างที่ 7.4 ในความเป็นจริงขณะกระทบพื้นมีความเร็ว ![]()
![]()
![]() เนื่องจากมีแรงต้านของอากาศ
จงหาแรงต้านเฉลี่ยของอากาศ
เนื่องจากมีแรงต้านของอากาศ
จงหาแรงต้านเฉลี่ยของอากาศ
วิธีทำ เนื่องจากแรงเสียดทานของอากาศมีผลน้อยมากต่อความเร็วของส้มดังนั้นงานที่เกิดจากแรงภายนอกสามารคำนวณได้จากนิยามของงาน
![]() =
= ![]()
![]() =
= ![]()
= ![]()
เครื่องหมายลบแสดงว่าแรงต้านอากาศมีทิศตรงข้ามกับการเคลื่อนที่ ฟิจารณารูปที่ 7.10 จากกฎการอนุรักษ์พลังงาน

รูปที่ 7.10
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าในสมการ
![]() =
= ![]()
= ![]()
พลังงานส่วนหนึ่งหายไปไหน
ตัวอย่างที่ 7.7 กล่องมวล
![]() เคลื่อนที่ลงตามทางโค้งลื่นสูง
เคลื่อนที่ลงตามทางโค้งลื่นสูง ![]() ดังรูปที่ 7.11 ที่ปลายทางโค้งต่อกับพื้นราบมีความเสียดทานยาว
ดังรูปที่ 7.11 ที่ปลายทางโค้งต่อกับพื้นราบมีความเสียดทานยาว ![]() ต่อจากนั้นเป็พื้นราบลื่นและเข้าชนสปริงทำให้สปริงหดเป็นระยะทาง
ต่อจากนั้นเป็พื้นราบลื่นและเข้าชนสปริงทำให้สปริงหดเป็นระยะทาง
![]() จงหาสัมปรสิทธ์ความเสียดทานระหว่างกล่องกับพื้นราบที่มีความเสียดทาน
จงหาสัมปรสิทธ์ความเสียดทานระหว่างกล่องกับพื้นราบที่มีความเสียดทาน
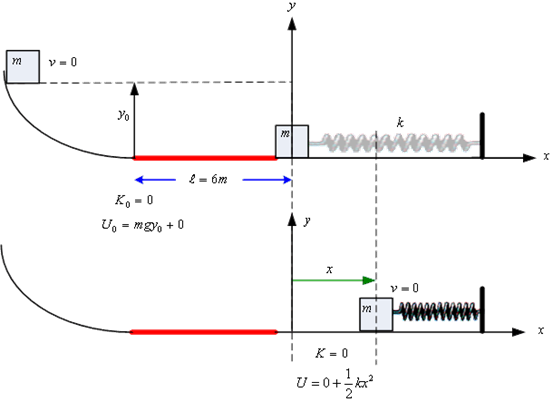
รุปที่ 7.11
วิธีทำ จากกฎการอนุรักษ์พลังงาน
![]() =
= ![]()
![]() =
= ![]()
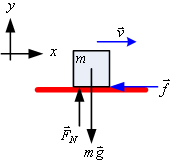
งานที่ระทำโดยแรงเสียดทานสามารถหาได้โดยอาศัยกฎข้อสองของนิวตันพิจารณารูปที่ 7.12
![]() =
= ![]()
รูปที่ 7.12 ![]() =
= ![]()
![]() =
= ![]()
จากนิยามสัมประสิทธิ์ความเสียดทานและความสัมพันธ์ระหว่างมวลแลน้ำหนัก
![]() =
= ![]()
![]() =
= ![]()
= ![]()
งานที่กระทำโดยแรงเสียดทาน (แรงไม่อนุรักษ์) สามารถหาได้โดยใช้นิยามของงาน
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
แทนค่า ![]() กลับลงในสใการที่ได้จากกฎการอนุรักษ์พลังงาน
เมื่อ
กลับลงในสใการที่ได้จากกฎการอนุรักษ์พลังงาน
เมื่อ ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
สรุป
กฎการอนุรักษ์พลังงาน : พลังงานสามารถเปลี่ยนจารูปหนึ่งไปยังอีกรูปหนึ่งได้ โดยที่ผลรวมของพลังงานทั้งหมดจะคงที่
กฎการอนุรักษ์พลังงาน ![]()
นิยามพลังงานศักย์ ![]()
พลังงานศักย์โน้มถ่วง ![]()
พลังงานศักย์สปริง ![]()