 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 8 ระบบอนุภาค
โดยปกติอนุภาค กลุ่มอนุภาคหรือวัตถุ มักไม่อยู่โดดเดี่ยวตามลำพังแต่จะอยู่ท่ามกลางอนุภาคอื่น ๆ หรือวัตถุอื่น ๆ และอาจจะมีอันตรกิริยา (interaction) กับสิ่งเหล่านั้น เช่นมีแรงดึงดูดซึ่งกันและกัน ทำให้ไม่สะดวกในการพิจารณาการเคลื่อนที่หรือเงื่อนไขของหลาย ๆ สิ่งพร้อมกัน จึงต้องเลือกพิจารณาเฉพาะส่วนที่สนใจแยกออกมาจากส่วนอื่น ๆ ส่วนที่เราเลือกพิจารณานั้น อาจเป็นอนุภาคเดี่ยวหรือกลุ่มอนุภาค วัตถุก้อนเดียวหรือหลาย ๆ ก้อนก็ตาม เรียกรวม ๆ กันว่าระบบ (system) แรงระหว่างอนุภาคหรือวัตถุภายในระบบเรียกว่า แรงภายใน ส่วนแรงระหว่างอนุภาคหรือวัตถุภายในระบบกับสิ่งต่าง ๆ นอกระบบเรียกว่า แรงภายนอก
ในบทนี้จะทำความเข้าใจเงื่อนไขต่าง ๆ ที่เกี่ยวข้องกับวัตถุเพื่ออธิบายถึงปรากฎการณ์ต่าง ๆ ที่เกิดขึ้นโดยการประยุกต์ใช้กฎข้อสองของนิวตันที่เกี่ยวข้องกับวัตถุและระบบอนุภาค โดยพิจารณาวัตถุในลักษณะต่างๆ รวมึงวัตุขนาดเล็ก จะทำให้เราทราบว่าทำไมจึงเป็นเช่นนี้คิดอย่างนี้ นอกจากนั้นยังอธิบายถึงโมเมนตัมเชิงเส้น และกฎการอนุรักษ์โมเมนตัมเชิงเส้น
เนื้อหาประกอบด้วย
8.1 กฎข้อสองของนิวตันและระบบอนุภาค
8.2 จุดศูนย์กลางมวล
8.3 นิยามของโมเมนตัมเชิงเส้น
8.4 กฎการอนุรักษ์โมเมนตัมเชิงเส้น
8.1 กฎข้อสองของนิวตันและระบบอนุภาค
เปรียบเทียบการโยนลูกเทนนิสกับดรัมเบล ให้เคลื่อนที่แบบโปรเจคไตล์ แนวการเคลื่อนทีของวัตถุทั้งสองเราจะพิจารณาที่ส่วนไหน หรือแรงที่กระทำจะคิดที่ตรงไหน ?
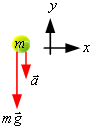 ปล่อยลูกเทนนิสตามแนวดิ่งตามรูปที่
8.1
ปล่อยลูกเทนนิสตามแนวดิ่งตามรูปที่
8.1
จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 8.1
จากเงื่อนไขการโยนลูกเทนนิสแรงที่กระทำบนลูกเทนนิสคือแรงโน้มถ่วงกระทำที่ลูกบอลโดยตรง แต่กระทำตรงส่วนไหน ? มวลก็ยังคงเป็นมวลของลูกบอลไม่เปลี่ยนแปลงส่วนความเร่งคืออัตราการเปลี่ยนแปลงความเร็วของลูกเทนนิส
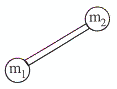 เปลี่ยนจากลูกเทนนิสเป็นดรัมเบลดังรูปที่
8.2 ซึ่งประกอบด้วยมวล 2 ก้อนและด้ามยึดระหว่างมวลทั้งสองเราจะคิดแรงกระทำที่ส่วนไหน
จะคิดที่มวลแต่ละก้อนกระทำต่อด้ามยึด หรือคิดที่ด้ามยึดกะทำต่อมวลแต่ละก้อน
จะใช้มวลก้อนไหนในการพิจารณา จะใช้มวลก้อนใดก้อนหนึ่ง
เปลี่ยนจากลูกเทนนิสเป็นดรัมเบลดังรูปที่
8.2 ซึ่งประกอบด้วยมวล 2 ก้อนและด้ามยึดระหว่างมวลทั้งสองเราจะคิดแรงกระทำที่ส่วนไหน
จะคิดที่มวลแต่ละก้อนกระทำต่อด้ามยึด หรือคิดที่ด้ามยึดกะทำต่อมวลแต่ละก้อน
จะใช้มวลก้อนไหนในการพิจารณา จะใช้มวลก้อนใดก้อนหนึ่ง
รูปที่ 8.2 หรือมวลทั้งสองหรือคิดทั้งหมด ส่วนน้ำหนักของดรัมเบลจะคิดที่ส่วนไหนจะคิดที่มวลแต่ละก้อน หรือที่ด้ามดรัมเบล ในส่วนของความเร่งจะพิจารณาที่มวลก้อนแรก ก้อนที่สองหรือคิดทั้งหมดให้ง่ายในการพิจารณาโดยอาศัยกฎข้อสองของนิวตัน
คำถามข้างต้นสามารถตอบได้โดยใช้แรงภายนอกเพียงแรงเดียวเท่านั้นคือน้ำหนัก ส่วนแรงภายในคือแรงที่ด้ามยึดกระทำต่อมวลแต่ละก้อนจะมีขนาดเท่ากันทิศตรงกันข้ามหักล้างกันหมดตามกฎข้อสามของนิวตัน ส่วนมวลคิดเป็นมวลรวมของทั้งระบบ และความเร่งให้คิดที่จุดจุดหนึ่งซึ่งเรียกว่าจุดศูนย์กลางมวล (center of mass, cm)
จากกฎข้อสองของนิวตัน
![]() =
= ![]()
ตัวอย่างที่ 8.1 เมื่อโยนดรัมเบลให้เคลื่อนที่แบบโปรเจคไตล์ ให้เขียนแนวทางการเคลื่อนที่ของดรัมเบลโดยใช้จุดศูนย์กลางมวล
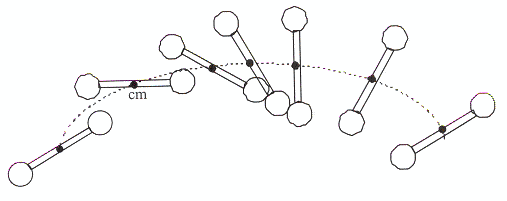 |
รูปที่ 8.3
8.2 จุดศูนย์กลางมวล
จุดศูนย์กลางมวลคือตำแหน่งเฉลี่ยของมวลของวัตถุทั้งก้อน พิจารณาวัตุมัลักษณะคล้าย
ดรัมเบล
จุดศูนย์กลางมวลบนแกน ![]() คือ
คือ
![]() =
= ![]()
= ![]()
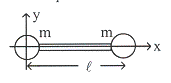 ตัวอย่างที่ 8.2 จงหาจุดศูนย์กลางมวลของดรัมเบลเมื่อวางบนแกน
ตัวอย่างที่ 8.2 จงหาจุดศูนย์กลางมวลของดรัมเบลเมื่อวางบนแกน
![]() ดังรูปที่ 8.4 สมมุติให้มวลทั้งสองมีค่าเท่ากันและไม่คิดมวลของด้ามดรัมเบล
ดังรูปที่ 8.4 สมมุติให้มวลทั้งสองมีค่าเท่ากันและไม่คิดมวลของด้ามดรัมเบล
วิธีทำ ![]() =
= ![]()
= ![]()
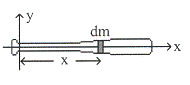 =
= ![]() =
= ![]()
สำหรับวัตถุรูปทรงใด ๆ จุดศูนย์กลางมวลสามารถคำนวณได้โดยการแบ่งวัตถุออกเป็นส่วนเล็ก
ๆ ![]() หลาย ๆ ชิ้น (ดังรูปที่ 8.5) แล้วนำส่วนเล็ก ๆ มารวมกันดังสมการ
หลาย ๆ ชิ้น (ดังรูปที่ 8.5) แล้วนำส่วนเล็ก ๆ มารวมกันดังสมการ
รูปที่ 8.5
![]() =
= ![]()
= 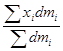
= ![]() =
= ![]()
ในกรณีวัตถุมีการกระจายมวลใน 2 มิติหรือ 3 มิติจะได้
![]() =
= ![]()
![]() =
= ![]()
นอกจากนี้จุดศูนย์กลางมวลยังสามารถเขียนอยู่ในรูปของเวกเตอร์ได้ดังนี้
![]() =
= ![]()
หรือ ![]() =
= 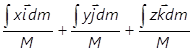
= ![]()
หรือ ![]() =
= ![]()
เมื่อ
![]() คือมวลส่วนเล็ก ๆ
ที่แบ่งจากมวลทั้งหมด
คือมวลส่วนเล็ก ๆ
ที่แบ่งจากมวลทั้งหมด ![]() จะได้
จะได้ ![]()
![]() คือปริมาตรส่วนเล็ก ๆ
คือปริมาตรส่วนเล็ก ๆ
ข้อสังเกตุ
![]() (ใช้กับวัตถุ
1 มิติ) เมื่อ
(ใช้กับวัตถุ
1 มิติ) เมื่อ ![]() คือความหนาแน่นต่อความยาวของวัตถุ
คือความหนาแน่นต่อความยาวของวัตถุ![]()
![]() (ใช้กับวัตถุ 2 มิติ) เมื่อ
(ใช้กับวัตถุ 2 มิติ) เมื่อ ![]() คือความหนาแน่นต่อพื้นที่ของวัตถุ
คือความหนาแน่นต่อพื้นที่ของวัตถุ
![]() (ใช้กับวัตถุ 3 มิติ) เมื่อ
(ใช้กับวัตถุ 3 มิติ) เมื่อ ![]() คือความหนาแน่นต่อปริมาตรของวัตถุ
คือความหนาแน่นต่อปริมาตรของวัตถุ
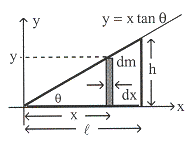 ตัวอย่างที่ 8.3 จงหาจุดศูนย์กลางมวลของวัตถุรูปทรงสามเหลี่ยมดังรูปที่
8.6
ตัวอย่างที่ 8.3 จงหาจุดศูนย์กลางมวลของวัตถุรูปทรงสามเหลี่ยมดังรูปที่
8.6
วิธีทำ เนื่องจากวัตถุเป็นรูปทรงสามเหลี่ยมวางอยู่ในระนาบ
![]() ดังรูปดังนั้นจุดศูนย์กลางมวลจะอยู่บนทั้งแกน
ดังรูปดังนั้นจุดศูนย์กลางมวลจะอยู่บนทั้งแกน
![]() และแกน
และแกน ![]()
แกน
![]() พิจารณาดังรูปที่ 8.6
พิจารณาดังรูปที่ 8.6
![]() =
= ![]()
รูปที่ 8.6 จากรูปแบ่งพื้นที่สามเหลี่ยมรูปใหญ่ออกเป็นพื้นที่รูปสี่เหลี่ยมเล็ก
ๆ มีมวล ![]() เมื่อมวลทั้งหมดของรูปสามเหลี่ยมคือ
เมื่อมวลทั้งหมดของรูปสามเหลี่ยมคือ
![]()
![]() =
= 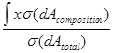
= 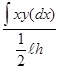
= ![]()
จากรูป ![]()
![]() =
= 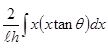
= 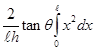
= 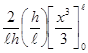
= 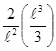 =
= ![]()
ถ้าไม่สนใจมุมที่พิจารณาจะได้จุดศูนย์กลางมวลของรูปสามเหลี่ยมบนแกน ![]() จะมีค่าเท่ากับ
จะมีค่าเท่ากับ ![]() โดยวัดจากจุดยอด (จุดที่ไม่ได้อยู่บนแกน
โดยวัดจากจุดยอด (จุดที่ไม่ได้อยู่บนแกน ![]() ) ดังนั้นจะได้
) ดังนั้นจะได้
![]() (วัดจากฐานอยู่บนแกน
(วัดจากฐานอยู่บนแกน ![]() )
)
การหาจุดศูนย์กลางมวลบนแกน
![]() ของรูปสามเหลี่ยม
ของรูปสามเหลี่ยม
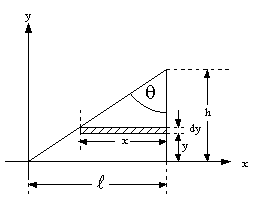
แกน
![]() พิจารณาดังรูปที่ 8.7
พิจารณาดังรูปที่ 8.7
![]() =
= ![]()
เมื่อ ![]() เป็นระยะที่วัดจากฐานสามเหลี่ยม
ขึ้นไป
เป็นระยะที่วัดจากฐานสามเหลี่ยม
ขึ้นไป
![]() =
= 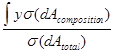
= ![]()
= ![]()
รูปที่ 8.7
จากรูป
![]()
![]() =
= ![]()
= 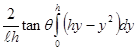
= 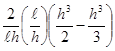
= 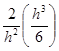 =
= ![]()
ดังนั้นจุดศูนย์กลางมวลของวัตถุรูปทรงสามเหลี่ยมคือ ![]()
กฎข้อที่สองของนิวตันสามารถแสดงโดยใช้เงื่อนไขจากจุดศูนย์กลางมวลได้ดังนี้
![]() =
= ![]()
![]() =
= ![]()
จากนั้นใช้เงื่อนไขของความเร็วและความเร่ง
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เปรียบเทียบกฎข้อสองของนิวตันเมื่อคิดจากมวลแต่ละก้อนกับระบบอนุภาค
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
ดังนั้นแรงลัพธ์ ![]() ที่เกิดจากมวลแต่ละก้อนของระบบอนุภาคคือแรงลัพธ์จากแรงภายนอก
เนื่องจากแรงกริยาและรงปฎิกริยาจะหักล้างกันหมด
ที่เกิดจากมวลแต่ละก้อนของระบบอนุภาคคือแรงลัพธ์จากแรงภายนอก
เนื่องจากแรงกริยาและรงปฎิกริยาจะหักล้างกันหมด
![]() =
= ![]()
8.3 นิยามของโมเมนตัม
จากกฎข้อที่สองของนิวตัน
![]() =
= ![]()
= ![]()
ถ้าให้มวลของวัตถุคงที่เราสามารเขียนใหม่ได้เป็น
![]() =
= ![]()
ค่าที่อยู่ในวงเล็บเรียกว่าโมเมนตัม
นิยามโมเมนตัมเชิงเส้น
![]() =
= ![]()
กฎข้อสองของนิวตันเมื่อเขียนอยู่ในรูปของโมเมนตัม
![]() =
= ![]() (พื้นฐานกฎข้อสองของนิวตัน)
(พื้นฐานกฎข้อสองของนิวตัน)
กฎข้อนี้สามารถนำไปประยุกต์ใช้กับระบบที่มวลแปรค่าได้ดี
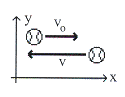 ตัวอย่างที่ 8.4
ลูกเทนนิสมวล
ตัวอย่างที่ 8.4
ลูกเทนนิสมวล ![]() เคลื่อนที่ในแนวเส้นตรงด้วยความเร็ว
เคลื่อนที่ในแนวเส้นตรงด้วยความเร็ว
![]() เข้ากระทบไม้เทนนิสแล้วสะท้อนกลับในแนวเดิมด้วยความเร็ว
เข้ากระทบไม้เทนนิสแล้วสะท้อนกลับในแนวเดิมด้วยความเร็ว
![]() ดังรูปทึ่ 8.8 ถ้าลูกเทนนิสกระทบไม้ในเวลา
ดังรูปทึ่ 8.8 ถ้าลูกเทนนิสกระทบไม้ในเวลา ![]() จงหา
จงหา
ก.โมเมนตัมเริ่มต้น
ข. โมเมนตัมสุดท้าย
ค. แรงเฉลี่ยที่กระทำต่อลูกเทนนิส
รูปที่ 8.8
วิธีทำ ก. จากนิยามของโมเมนตัมเชิงเส้น
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
ข. จากนิยามของโมเมนตัมเชิงเส้น
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
เมื่อโมเมนตัมเป็นปริมาณเวกเตอร์ ดังนั้นความเร็วปลายมีทิศตรงข้ามกับความเร็วต้น จึงมีเครื่องหมายเป็นลบ
ค. การประยุกต์ใช้กฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
แรงจะกระทำต่อลูกเทนนิสไปทางซ้ายมือ ทางแกน ![]()
8.4 กฎการอนุรักษ์โมเมนตัมเชิงเส้น
วัตถุส่วนมากที่พิจารณาจะถูกแรงภายนอกกระทำ ในกรณีที่ไม่มีแรงภายนอกมากระทำกับวัตถุ จากกฎข้อสองของนิวตัน
![]() =
= ![]()
เมื่อไม่มีแรงภายนอกมากระทำ
![]() =
= ![]() =
= ![]()
นั่นคือโมเมนตัมเชิงเส้นไม่มีการเปลี่ยนแปลง (คงที่)
กฎการอนุรักษ์โมเมนตัมเชิงเส้น "ผลรวมของโมเมนตัมเชิงเส้นของวัตถุ ก่อนการเปลี่ยนแปลงกับภายหลังการเปลี่ยนแปลงจะมี่ค่าคงที่
ตัวอย่างที่
8.5 มนุษย์อวกาศหนัก
![]() ขว้างประแจหนัก
ขว้างประแจหนัก ![]() ออกไปด้วยความเร็ว
ออกไปด้วยความเร็ว ![]() ดังรูปที่ 8.9 จงคำนวณหาความเร็วสะท้อนกลับของมนุษย์อวกาศ
ดังรูปที่ 8.9 จงคำนวณหาความเร็วสะท้อนกลับของมนุษย์อวกาศ
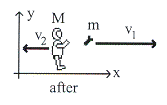
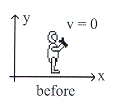
รูปที่ 8.9
วิธีทำ พิจารณาระบบประกอบด้วยมนุษย์อวกาศและประแจก่อนการเปลี่ยนแปลง (อยู่รวมกัน) และภายหลังการเปลี่ยนแปลง (แยกจากกัน) เมื่อระบบมีการเปลี่ยนแปลงคือมีแรงที่มนุษย์อวกาศกระทำต่อประแจเพียงแรงเดียว แรงนี้จะมีค่าเท่ากับแรงที่ประแจกระทำต่อมนุษย์อวกาศแต่มีทิศตรงกันข้าม จากกฎการอนุรักษ์โมเมนตัมเชิงเส้นจะได้
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
ตัวอย่างที่
8.6 นิวตรอนวิ่งด้วยความเร็ว
![]() เข้าชนดิวเทอรอน
เข้าชนดิวเทอรอน ![]() ทำให้เกิดการแตกตัวกลายเป็นนิวตรอนและโปรตรอน
โดยที่นิวตรอนตัวแรกยังคงวิ่งไปในทิศทางเดิมและมีความเร็ว
ทำให้เกิดการแตกตัวกลายเป็นนิวตรอนและโปรตรอน
โดยที่นิวตรอนตัวแรกยังคงวิ่งไปในทิศทางเดิมและมีความเร็ว ![]() ส่วนนิวตรอนตัวที่สองทำมุม
ส่วนนิวตรอนตัวที่สองทำมุม ![]() กับแนวระดับและมีความเร็ว
กับแนวระดับและมีความเร็ว ![]() ดังรูปที่ 8.10 จงหาความเร็วของโปตรอน กำหนดให้มวลของโปรตรอนและนิวตรอนมีค่าเท่ากัน
ดังรูปที่ 8.10 จงหาความเร็วของโปตรอน กำหนดให้มวลของโปรตรอนและนิวตรอนมีค่าเท่ากัน

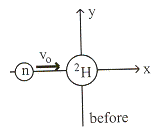
รูปที่ 8.10
วิธีทำ โมเมนตัมเป็นปริมาณเวกเตอร์
ดังนั้นในการคำนวณต้องพิจารณาทิศการเคลื่อนที่ตามแกน ![]() และ
และ ![]()
โมเมนตัมก่อนชน (ก่อนการเปลี่ยนแปลง)
แกน
![]()
![]() =
= ![]()
แกน
![]()
![]() =
= ![]()
โมเมนตัมหลังชน (ภายหลังการเปลี่ยนแปลง)
แกน
![]()
![]() =
= ![]()
แกน
![]()
![]() =
= ![]()
จากกฎการอนุรักษ์โมเมนตัมเชิงเส้น
![]() =
= ![]()
แกน
![]()
![]() =
= ![]()
![]() =
= ![]()
แกน
![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]() ………… (1)
………… (1)
![]() =
= ![]()
= ![]() …………. (2)
…………. (2)
จากสมการที่ 1 และ 2 จะสังเกตุเห็นว่าความเร็วทั้งสองเป็นองค์ประกอบของความเร็วในแกน
![]() และ
และ ![]() ดังนั้นความเร็วลัพธ์คือ
ดังนั้นความเร็วลัพธ์คือ
![]() =
= ![]()
= ![]()
= ![]()
มุมที่ความเร็ว
![]() กระทำกับแนวราบ
กระทำกับแนวราบ
![]() =
= 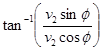
= ![]()
= ![]()
การคำนวณโดยใช้กฎการอนุรัษ์โมเมนตัมไม่จำเป็นต้องทราบข้อมูลที่เกี่ยวข้องกับแรงที่มากระทำ
สรุป
กฎข้อสองของนิวตันสำหรับระบบอนุภาค : ![]()
นิยามจุดศูนย์กลางมวล : ![]()
นิยามโมเมนตัมเชิงเส้น : ![]()
กฎพื้นฐานข้อสองของนิวตัน : ![]()
กฎการอนุรักษ์โมเมนตัมเชิงเส้น : ![]()