บทที่  10 การหมุน

          บทที่ผ่านมาจะกล่าวถึงจลศาสตร์  แรง  พลังงาน  และโมเมนตัม  ซึ่งจะอธิบายเกี่ยวกับกฎพื้นฐานของการเคลื่อนที่  และกฎการอนุรักษ์  ซึ่งจะพิจารณาเฉพาะวัตถุที่เคลื่อนที่ในแนวเส้นตรงเท่านั้น  แต่ในนความเป็นจริงการหมุนก็เป็นการเคลื่อนที่อีกแบบหนึ่ง  ซึ่งในบทนี้และบทต่อไปจะอธิบายเกี่ยวกับการหมุน

เนื้อหาประกอบด้วย

10.1   นิยามการหมุน                        10.2  จลศาสตร์การหมุน

10.3         กฎการหมุน                       10.4  ทฤษฎีแกนตั้งฉากและทฤษฎีแกนขนาน

10.5         รัศมีไจเรชั่น                       10.6  การประยุกต์ใช้กฎการหมุน

10.7 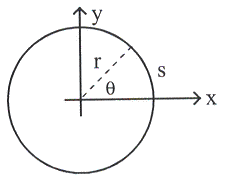        พลังงานจลน์ในการหมุน

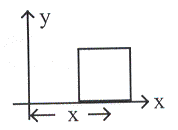
10.1 นิยามการหมุน

 

 

 

 

 

 

                                      ก.                                                        ข.

 

รูปที่  10.1

 

          เปรียบเทียบความคล้ายคลึงระหว่างการเคลื่อนที่เชิงเส้นกับการเคลื่อนที่เชิงมุม  โดยพิจารณาดังรูปที่ 10.1  ก. และ  ข.

 

การเคลื่อนที่เชิงเส้น	การเคลื่อนที่เชิงมุม
ตำแหน่ง : จะบอกด้วยระยะทางซึ่งวัดจากแกนอ้างอิงมุมฉากถึงตำแหน่งที่วัตถุอยู่	มุม : จะบอกด้วยมุมซึ่งวัดจากแกนอ้างอิงมุมฉากถึงตำแหน่งที่วัตถุอยู่
การกระจัดชิงเส้น : การเปลี่ยนแปลงตำแหน่ง	การกระจัดเชิงมุม : การเปลี่ยนแปลงมุม
ความเร็ว : การกระจัดที่เปลี่ยนไป	ความเร็วเชิงมุม : การกระจัดเชิงมุมที่เปลี่ยนไป
ความเร่ง : การเปลี่ยนแปลงความเร็ว	ความเร่งเชิงมุม : การเปลี่ยนแปลงความเร็วเชิงมุม

 

          เปรียบเทียบความสัมพันธ์ระหว่างการเคลื่อนที่เชิงเส้นกับการเคลื่อนที่เชิงมุมในรูปของสมการทางคณิตศาสตร์

 

การเคลื่อนที่เชิงเส้น	การเคลื่อนที่เชิงมุม	ความสัมพันธ์
ตำแหน่ง :	มุม :
การกระจัด :	การกระจัดเชิงมุม :
ความเร็ว :	ความเร็วเชิงมุม :
ความเร่ง :	ความเร่งเชิงมุม :

 

ตัวอย่างที่  10.1  แผ่น  CD  มีเส้นผ่าศูนย์กลาง   วางอยู่บนแป้นหมุนซึ่งอยู่นิ่ง  เมื่อกดให้สวิทซ์ทำให้แผ่น  CD  หมุนด้วยความเร็ว  200 rpm  ภายในเวลา   จงหา

ก.     ความเร่งเชิงมุมเฉลี่ย

ข.     ถ้าแผ่น  CD  มีความเร็วลดลงเหลือ  100 rpm  จงหาความเร่งเชิงเส้น

 

 

วิธีทำ  เปลี่ยนความเร็วเชิงมุมจากหน่วย rpm (รอบต่อนาที) ให้เป็นหน่วย  rad/s

                        =      

                             =      

                         =      

                             =      

ก.     จากสมการ

      =           =           =      

 

          =      

          =      

ข.     จากความสัมพันธ์ระหว่างความเร่งเชิงมุมกับความเร่งในแนวเส้นสัมผัส

      =            =      

          =      

ค.     จากความสัมพันธ์ระหว่างความเร็วเชิงมุมกับความเร่งเข้าสู่ศูนย์กลาง

      =           =      

          =      

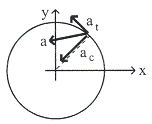
          พิจารณารูปที่  10.2  จะได้ความเร่งเชิงเส้นของแผ่น  CD  คือ

                 =      

                   =      

                   =      

 

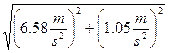
   รูปที่  10.2

 

 

 

10.2 จลศาสตร์การหมุน

การเคลื่อนที่เชิงเส้นของวัตถุด้วยความเร่ง    คงที่  สมการเหล่านี้ได้มาจากการ integrate ชุดสมการจลศาสตร์ดังนี้

 

                  

 

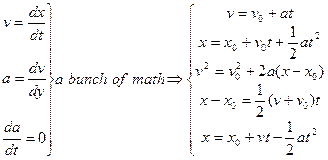
เมื่อพิจารณาสัญลักษณ์ที่ใช้แทนการเคลื่อนที่เชิงเส้นและเชิงมุมเช่น  กับ  ; กับ  เป็นต้น มาเปรียบเทียบกับสมการการเคลื่อนที่เชิงเส้นเมื่อ   คงที่  เราจะได้สมการการเคลื่อนที่เชิงมุมของวัตถุเมื่อ    คงที่ดังนี้

 

 

         

 

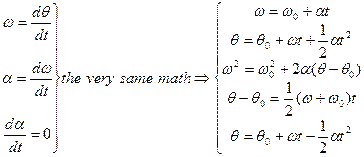
          การใช้สมการการเคลื่อนที่เชิงเส้นใช้ได้เมื่อ    คงที่  ในทำนองเดียวกับสมการการหมุนใช้ได้เมื่อ    คงที่

 

ตัวอย่างที่  10.2  จากตัวอย่างที่ 10.1  จงหา

ก.     แผ่น CD  หมุนได้กี่รอบจึงจะหยุดหมุน

ข.     ระยะทางเชิงเส้นที่แผ่น  CD  เคลื่อนที่ได้ก่อนที่จะหยุดหมุน

วิธีทำ    ก.  จาก                         =      

จากตัวอย่างที่  10.1  เมื่อ    ;   ;    ;    ;    ; 

                          =      

                             =      

                             =      

                             =      

ข.                       =      

                             =      

                             =      

 

10.3 การหมุน

กฎการเคลื่อนที่ของนิวตันใช้ได้ดีกับการเคลื่อนที่ของวัตถุ  ทำนองเดียวกันเราใช้กฎการเคลื่อนที่ของนิวตันกับการหมุนด้วย

กฎข้อที่หนึ่งของนิวตันสำหรับการหมุน

วัตถุทุกชนิดจะเคลื่อนที่ด้วยความเร็วเชิงมุมคงที่  นอกจากมี แรง ทอร์ดมากระทำต่อวัตถุนั้น

ล้อรถจักรยานจะไม่สามารถเคลื่อนที่ได้นอกจากมีแรงภายนอกมากระทำ  บางแรงทำให้ล้อหมุนแต่บางแรงไม่มีผลต่อการหมุน

ทอร์คคืออะไรและต่างจากแรงอย่างไร

 

                     

 

 

 

 

 

 

 

 

 

 

 

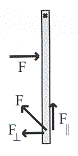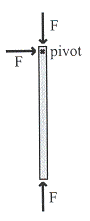
รูปที่  10.3                                   รูปที่  10.4

 

          พิจารณารูปที่ 10.3 จะสังเกตุเห็นว่าแนวแรงที่กระทำต่อไม้เมตรผ่านจุดหมุน (pivot) กรณีนี้จะไม่เกิดการหมุน  แต่ถ้าแนวแรงที่กระทำต่อไม้เมตรไม่ผ่านจุดหมุน  กรณีนี้จะเกิดการหมุน  นอกจากนี้แรงที่กระทำต่อไม้เมตรสามารถแยกออกเป็นองค์ประกอบย่อยเป็นแรงที่ตั้งฉากกับไม้เมตรและแรงที่ชนานกับไม้เมตรดังรูปที่  10.4  แรงที่มีผลต่อการหมุนคือแรงที่ตั้งฉากกับไม้เมตรเท่านั้น  นั่นคือ

                          =           =      

                             =      

                             =      

          เมื่อ    คือผลคูณระหว่างระยะทางที่ลากจากจุดหมุนมาตั้งฉาก (แขนหมุน) กับแนวแรง  หรือผลคูณระหว่างแรงที่ตั้งฉากกับแขนหมุน  ดังรูปที่ 10.5

         

 

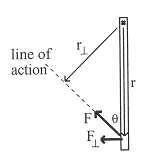
ทอร์คเมื่อเขียนอยู่ในรูปของเวกเตอร์  หรือ  cross product                       =      

การหาทิศของทอร์คจะกล่าวในบทต่อไป

 

 

 

 

 

 

                   รูปที่  10.5

 

 

 

          ตัวอย่างที่ 10.3  ออกแรงในแนวดิ่ง  เพื่อเปิดฝากระป๋องสีโดยออกแรงห่างจากจุดหมุนเป็นระยะ  ดังรูปที่ 10.6  จงหา

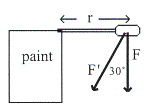
ก. ขนาดของทอร์ค

ข. แรง  ที่ต้องใช้เปิดฝากระป๋องเมื่ออกแรงทำมุม       กับแนวดิ่ง

วิธีทำ  ก. เนื่องจากแรงที่ออกตั้งฉากกับแขนหมุนจะได้ว่า

                                    =      

ขนาดของทอร์ค                 =      

                                      =      

                                      =      

ข.เมื่อแรง   ไม่ตั้งฉากกับแขนหมุน  เมื่อแยกองค์ประกอบของแรงจะมีเพียงแรงเดียวเท่านั้นที่มีผลต่อการหมุน แรงนั่นคือ    จะได้ว่า

                                    =      

                                    =      

                                  =      

                                      =      

 

กฎข้อสองของนิวตันสำหรับการหมุน

          ความเร่งเชิงมุมของวัตถุจะเปลี่ยนแปลงตามค่าทอร์ค  แต่ไม่ขึ้นกับโมเมนต์ความเฉื่อยของวัตถุ

          จาก                =        

                                =            เมื่อ    คือโมเมนต์ความเฉื่อย

กฎข้อสองสำหรับการหมุน

                                =      

โมเมนต์ความเฉื่อยคืออะไร  ใช้ทำอะไรมีผลอย่างไร  และจะคำนวณอย่างไร

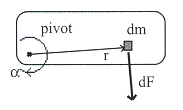          วัตถุรูปทรงใด ๆ แขวนอยู่ดังรูปที่  10.7  โดยมีความเร่งเชิงมุม    พิจารณามวลก้อนเล็ก ๆ  ถูกกระทำด้วยแรง     ซึ่งตั้งฉากกับแขนหมุนทำให้    มีความเร่งเชิงมุม     ด้วย  อาศัยสมการ

       =           จะได้ว่า

     =      

แต่    คือแรงในแนวเส้นสัมผัส แทนด้วย  จะได้ความเร่งในแนวเส้นสัมผัส       ด้วย

            รูปที่  10.7                       

                                  =          =      

                                      =      

                                      =      

                                =      

                                    =      

          เปรียบเทียบสมการที่ได้กับกฎข้อสองของการหมุนเมื่อ    ที่ได้คือผลรวมของทอร์คทั้งหมดที่เกิดจากมวลย่อย ๆ    จะได้ค่าโมเมนต์ความเฉื่อยของวัตถุรูปทรงใด ๆ คือ

                                    =      

          ตามปกติความเฉื่อยต่อการเลื่อนตำแหน่งของวัตถุขึ้นอยู่กับมวล  แต่ความเฉื่อยต่อการหมุน (โมเมนต์ความเฉื่อย)  จะไม่ขึ้นกับมวลแต่ขึ้นอยู่กับรูปทรงของวัตถุ

 

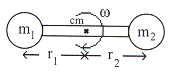ตัวอย่างที่ 10.4  ดรัมเบลประกอบด้วยมวลก้อนละ    เชื่อมด้วยมวลเบายาว    หมุนรอบแกนซึ่งตั้งฉากกับระนาบของกระดาษดังรูปที่ 10.8  จงหาขนาดของทอร์คที่ทำให้ดรัมเบลหมุนด้วยความเร็ว    และหยุดภายในเวลา 

วิธีทำ  ถือว่ามวล    ทั้งสองมีขนาดเล็กเมื่อเทียบกับระยะทางระหว่างมวลทั้งสอง  ดังนั้นค่าโมเมนต์ความเฉื่อยจากเงื่อนไขการอินทิเกรตก็คือผลรวมของมวลทั้งหมด

       =                 =      

          รูปที่  10.8                แทนค่าต่าง ๆ ในสมการ

                                    =      

                                      =      

                                      =      

แต่                               =           =      

                                      =      

                                      =      

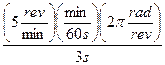
จากกฎข้อสองของการหมุน

                                =      

                                    =      

                                      =      

                                      =      

          ในกรณีที่วัตถุมีรูปทรง  รัศมีในการหมุนวัดจากจุดหมุนไปยังมวลส่วนเล็ก ๆ มีค่าไม่มากนักเมื่อเทียบกับขนาดของวัตถุ  เราสมารถคำนวณหาโมเมนต์ความเฉื่อยได้โดยการอินทิเกรต

 

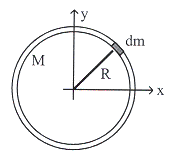
ตัวอย่างที่  10.5  ก. จงหาโมเมนต์ความเฉื่อยของวงแหวนบางสม่ำเสมอรัศมี    มวล    รอบแกนที่ผ่านจุดศูนย์กลางมวลดังรูปที่ 10.9

ข.  จงหาโมเมนต์ความเฉื่อยของแผ่นจานบางสม่ำเสมอรัศมี   มวล    รอบแกนที่ผ่านจุดศูนย์กลางมวลดังรูปที่ 10.10

 วิธีทำ  ก. แบ่งวงแหวนออกเป็นส่วนเล็ก ๆ มีมวล    ห่างจากแกนหมุนรัศมี    โมเมนต์ความเฉื่อยของมวล  คือ         

    =      

=      

          =      

=      

เมื่อผลรวมทั้งหมดของมวล    ที่แบ่งเป็นส่วนเล็ก ๆ มีค่าเท่ากับ    ดังนั้นจะได้ว่าโมเมนต์ความเฉื่อย

              ของวงแหวนบางรอบจุดศูนย์กลางมวลคือ

                             =      

รูปที่  10.10    

ข. ในกรณีเป็นแผ่นจานเมื่อแบ่งแผ่นจานออกเป็นวงแหวนเล็ก ๆ รัศมี    หนา    มีมวล    จะสังเกตุเห็นว่า  ค่าขอบของวงแหวนมีค่าไม่คงที่จะเปลี่ยนตามระยะ    ดังนั้นค่าโมเมนต์ความเฉื่อยของแผ่นจานเกิดจากโมเมนต์ความเฉื่อยส่วนเล็ก ๆ ของวงแหวน    ดังรูปที่ 10.10

 

 

 

 

 

    

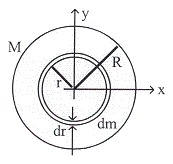
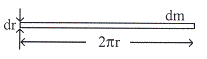
       เมื่อนำมวล  หนา   มาคลี่

 

 

      รูปที่  10.10

 

                                   =      

เมื่อรวมวงแหวนส่วนเล็ก ๆ ทั้งหมดก็จะกลายเป็นแผ่นบาง

                                =      

                                 =      

          แต่มวลส่วนเล็ก    ขึ้นอยู่รัศมี  สมมติเป็นแผ่นจานบางสม่ำเสมอดังนั้นการกระจายของมวลจะขึ้นอยู่กับพื้นที่

                                 =          เนื่องจาก    ขึ้นอยู่กับพื้นที่

                                  =      

 

หรือคำนวณหาจาก         =              =         

แต่     คือความหนาแน่นต่อพื้นที่จะได้     จากบทที่ 8

                                          =         

                                                =         

                                                =         

 

 

แทนค่า     ลงในสมการ

                                 =      

                                      =      

                                 =      

                                      =      

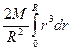
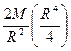
โมเมนต์ความเฉื่อยของแผ่นจานกลมรอบจุดศูนย์กลางคือ

                                       =      

          จากค่าโมเมนต์ความเฉื่อยที่ได้ถ้าปล่อยวงแหวนกับแผ่นจานให้กลิ้งลงจากพื้นเอียงอันไหนจะถึงปลายพื้นเอียงก่อน

          ค่าโมเมนต์ความเฉื่อยของวัตถุขึ้นอยู่กับรูปร่างของวัตถุแสดงดังตารางที่  10.1

 

ตารางที่  10.1

 

10.4   ทฤษฎีแกนตั้งฉากและทฤษฎีแกนขนาน

ในบางกรณีการคำนวณค่าโมเมนต์ความเฉื่อยมีความยุ่งยากซับซ้อนเราสามารถทำให้ง่ายขึ้นโดยใช้ทฤษฎีแกนตั้งฉาก  หรือทฤษฎีแกนขนานเข้ามาช่วย

 

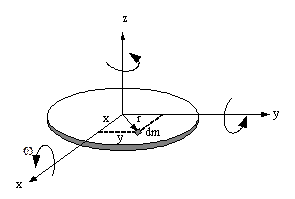10.4.1  ทฤษฎีแกนตั้งฉาก  เป็นทฤษฎีที่ใช้ในการคำนวณหาค่าโมเมนต์ความเฉื่อยของวัตถุแข็งเกร็งที่มีลักษณะเป็นแผ่นบาง ๆ พิจารณาวัตถุหมุนรอบแกน   ,  และ   แสดงดังรูปที่ 10.11

 

 

        

 

 

 

 

 

 

 

 

 

                                รูปที่ 10.11    

 

จาก                               =      

เมื่อ    เป็นระยะจาก    ถึงแกน   และ   เนื่องจากเป็นวัตถุแผ่นบางจะได้

                                   =      

แต่     

 

                                   =      

                                      =      

                                   =      

 

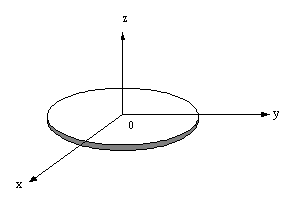ตัวอย่างที่ 10.6  จงหาค่าโมเมนต์ความเฉื่อยของแผ่นจานบางสม่ำเสมอมวล   รัศมี   รอบแกน    และ    ดังรูปที่ 10.12

 

 

 

 

 

 

 

 

 

 

 

 

รูปที่  10.12

 

 

 

วิธีทำ  อาศัยแกน   ,  และ    ตามรูป  ให้ระนาบของวงกลมอยู่ในระนาบ    และจุดศูนย์กลางอยู่ที่จุด    จะได้

 

 

 

                            

 

 

 

 

 

 

 

 

 

 

      =      

แต่    และ    จะได้ 

                                 =      

                                   =      

 

และ                            =      

นั่นคือ 

 

10.4.2  ทฤษฎีแกนขนาน  ค่าโมเมนต์ความเฉื่อยของวัตถุโดยทั่ว ๆ ไปเราจะทราบค่าโมเมนต์ความเฉื่อยของวัตถุรอบแกนที่ผ่านจุดศูนย์กลางของมวลของวัตถุ  ถ้าต้องการจะหาค่าโมเมนต์ความเฉื่อยของวัตถุนั้นรอบแกนหมุนใด ๆ ซึ่งขนานกับแกนหมุนที่ผ่านจุดศูนย์กลางมวล  และห่างออกมาเท่ากับ    ดังรูปที่ 10.13

 

 

 

 

 

 

 

 

 

 

รูปที่  10.13

 

 

 

                                   =      

เมื่อ

            คือโมเมนต์ความเฉื่อยรอบแกนใด ๆ ที่ขนานกับแกนที่ผ่านจุดศูนย์กลางมวล

           คือโมเมนต์ความเฉื่อยรอบจุดศูนย์กลางมวล

            คือมวลของวัตถุนั้น

            เป็นระยะห่างระหว่างแกนทั้งสอง

 

ตัวอย่างที่  10.7  จงใช้ทฤษฎีแกนขนานหาค่าโมเมนต์ความเฉื่อยของลวดเส้นเล็ก  มวล   ยาว   ซึ่งหมุนรอบจุด    ที่อยู่ปลายลวดดังรูปที่  10.4 

 

 

 

 

 

 

 

 

 

 

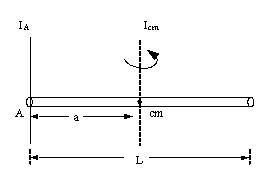
รูปที่  10.4

 

 

วิธีทำ                                     =      

                                                =      

                                                =      

                                                =      

                                                =      

 

10.5 รัศมีไจเรชั่น

จากตัวอย่างที่ผ่านมา  เราจะพบว่าวัตถุที่มีรูปร่างต่างๆ กันย่อมมีสมการโมเมนต์ความเฉื่อยต่างกัน  ดังนั้นเพื่อความสะดวกในการคำนวณ   จึงได้มีการกำหนดสมการทั่วไปสำหรับโมเมนต์ของความเฉื่อยของวัตถุทุกรูปร่างขึ้นมาเมื่อ

                                      =      

เมื่อ                   คือโมเมนต์ความเฉื่อยของวัตถุทุกรูปร่าง

                        คือมวลของวัตถุนั่น

                        คือรัศมีไจเรชั่น

 

 

 

 

 

 

 

10.6 การประยุกต์ใช้กฎการหมุน

ตัวอย่างที่  10.8  แขวนมวล   =   ที่ปลายเชือกเบาโดยปลายอีกข้างหนึ่งคล้องผ่านรอกมวล    =     มีเส้นผ่าศูนย์กลาง    แสดงดังรูปที่    จงหาความเร่งของมวลที่แขวน

 

 

 

 

 

 

 

 

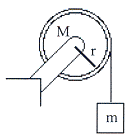
                                          รูปที่  10.14

 

วิธีทำ  เพื่อความสะดวกในการคำนวณให้แยกคิดที่ละส่วนดังนี้

          พิจารณาแรงที่กระทำบนมวลที่แขวน  เมื่อมวลเคลื่อนที่ในแนวเส้นตรง  อาศัยกฎการเคลื่อนที่ข้อสองของนิวตัน  ตามรูปที่  10.15

                     =      

                   =      

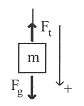
                   =                     (1)

          กำหนดให้ทิศลงมีเครื่องหมายเป็นบวก

 

รูปที่  10.15              พิจารณาแรงที่กระทำต่อรอก  ซึ่งประกอบด้วยแรง   ;   และ    ดังรูปที่ 10.16  แรงที่ทำให้เกิดทอร์คและทำให้รอกหมุนคือแรง    เท่านั้น  กำหนดให้ทิศหมุนตามเข็มนาฬิกาเป็นบวก

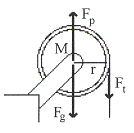จากกฎข้อสองของการหมุน

   =      

               =      

                =      

          แทนค่า     ลงในสมการที่  1  จะได้ 

                 =                     (2)

                 รูปที่  10.16

 

          เมื่อ    คือโมเมนต์ความเฉื่อยของแผ่นจานกลมกลมรอบจุดศูนย์กลางมวลจะได้    เมื่อความเร่ง    คือความเร่งที่เกิดเนื่องจากจากแรง    เป็นความเร่งที่ขอบที่ขอบของแผ่นจานกลมดังนั้น    แต่    แทนค่าต่างๆ ลงในสมการที่  (2)

                          =      

                                 =      

                               =      

                                             =      

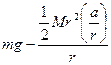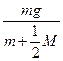
แทนค่าต่าง ๆ เพื่อหาค่า 

                                    =      

                                      =         

 

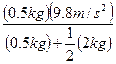
ตัวอย่างที่ 10.9  วัตถุทรงกลมมวล    รัศมี    มีโมเมนต์ความเฉื่อย    กลิ้งลงมาตามพื้นเอียงสูง    จงหาความเร่งและความเร็วเชิงเส้นที่ปลายพื้นเอียง

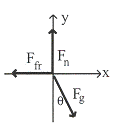
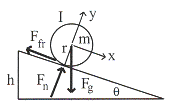วิธีทำ

 

 

 

 

 

 

 

รูปที่  10.17

 

เขียน  free  body  diagram  แสดงแรงที่กระทำกับวัตถุแสดงดังรูปที่  10.17  จะสังเกตเห็นว่าแรงที่ทำให้หมุนคือแรงเสียดทาน  จากกฎการเคลื่อนที่ข้อ  2  ของนิวตัน  เมื่อแยกพิจารณาในแต่ละส่วน

พิจาณาการเลื่อนตำแหน่ง

แกน 

                                       =      

                              =      

                             =                               (1)

(เมื่อแรง    เป็นแรงที่ทำให้วัตถุทรงกลมหมุนหมุน)

แกน                               =      

                               =      

                                                       =                              (2)

 

พิจารณาการหมุน

                                         =      

                                         =      

                                           =                               (3)

แทนสมการที่  (3)  ลงในสมการที่  (1)

                             =      

          แต่    คือความเร่งในแนวเส้นสัมผัส  อาศัยความสัมพันธ์ระหว่างความเร่งเชิงเส้นในแนวเส้นสัมผัสกับความเร่งเชิงมุมจะได้ 

          พิจารณาการเลื่อนตำแหน่งของวัตถุทรงกลมอย่างเดียวแสดงดังรูปที่ 10.17  ก.  และการหมุนอย่างเดียวแสดงดังรูปที่  10.17  ข.  เพื่อใช้ประกอบการรพิจารณาการเคลื่อนที่ของวัตถุว่าเป็นการเคลื่อนที่ลักษณะใด  ถ้าเคลื่อนที่แบบกลิ้งเป็นการเคลื่อนรวมกันทั้งสองแบบ

 

 

 

 

 

 

 

 

 

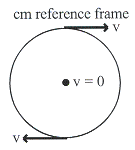
       ก. วัตถุเลื่อนตำแหน่งอย่างเดียว                  ข.  วัตถุหมุนอย่างเดียว

 

รูปที่ 10.17  แสดงการเคลื่อนที่ของทรงกลม

 

                          =      

                             =      

                                 =      

                                             =      

 

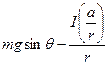          จากสมการที่ได้ถ้าวัตถุไม่มีการหมุน    จะได้คำตอบของความเร่งคือ    ซึ่งกล่าวมาแล้วจากข้างต้น

          เนื่องจากความเร่ง    ที่ได้เป็นค่าคงที่  ดังนั้นเราสามารถคำนวณหาค่าความเร็วของวัตถุทรงกลม  จากโจทย์ค่าต่าง ๆ ที่กำหนดให้มีดังนี้

                     ;    ;    ;    (ต้องการหา)

                     ; 

          จากค่าที่กำหนดให้สมการการเลื่อนตำแหน่งที่ไม่ติดตัวแปรเวลา    คือ

 

 

 

                                   =      

                                      =      

                                      =      

                                    =      

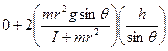
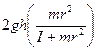
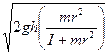
          นั่นคือถ้าวัตภุไม่มีการหมุน    คำตอบของความเร็วคือ    ตามที่ได้กล่าวมาแล้ว

          สรุป  ทอร์คจะอธิบายถึงการหมุนของวัตถุ  ส่วนแรงจะอธิบายถึงการเลื่อนตำแหน่งของวัตถุ

 

10.7 พลังงานจลน์ในการหมุน

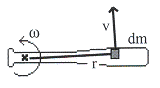จากบทที่ผ่าน ๆ มา  หัวข้อสุดท้ายที่จะกล่าวถึงคือกฎการอนุรักษ์พลังงาน  เนื่องจากเมื่อใช้พลังงานคำนวณจะทำให้ง่ายและสะดวกกว่าการคำนวณเมื่อใช้แรงและทอร์ค  แต่ปัญหาที่เกิดขึ้นคือพลังงานจนล์มีผลต่อการหมุนอย่างไร พิจารณาดังรูปที่ 10.18  เมื่อแบ่งมวลออกเป็นส่วนเล็ก ๆ   มีความเร็ว    และอยู่ห่างจากจุดหมุน    จากนิยามของพลังงานจลน์เชิงเส้นของมวลเล็ก ๆ

                 =      

 

          รูปที่ 10.18 

 

แต่    คือความเร็วในแนวเส้นสัมผัส    จะได้

                                  =      

คิดทั้งหมด

                                =         

          เมื่อสมการทางซ้ายมือคือพลังงานจลน์ในการหมุนของวัตถุทั้งก้อน  ส่วนสมการทางขวามือคือโมเมนต์ความเฉื่อย

          พลังงานจลน์ในการหมุน

                                    =      

 

          จะสังเกตุเห็นว่าพลังงานจลน์เชิงเส้นจะมีค่าเท่ากับครึ่งหนึ่งของผลคูณระหว่างความเฉื่อย (มวล)  กับความเร็วกำลังสอง  ในทำนองเดียวกันพลังงานจลน์ในการหมุนจะมีค่าเท่ากับครึ่งหนึ่งของผลคูณระหว่างโมเมนต์ความเฉื่อยและความเร็วเชิงมุมยกกำลังสอง

 

ตัวอย่างที่ 10.10  จากตัวอย่างที่ 10.9  จงหาความเร่งและความเร็วเชิงเส้นเมื่อใช้กฎการอนุรักษ์พลังงาน

วิธีทำ

 

 

 

 

 

 

 

 

 

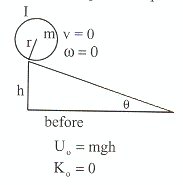
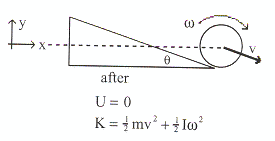
     รูปที่  10.19

พิจารณารูปที่ 10.19  เมื่อวัตถุกลิ้งพลังงานจลน์ที่เกี่ยวข้องได้แก่พลังงานจลน์เชิงเส้น (การเคลื่อนที่ของจุด cm)  กับพลังงานจลน์ในการหมุน (วัตถุหมุนรอบจุด cm)  จากกฎการอนุรักษ์พลังงาน

                                     =      

      =      

                                         =      

เมื่อวัตถุกลิ้งโดยไม่มีการไถลความเร็วเชิงเส้นจะสัมพันธ์กับความเร็วเชิงมุมดังนี้

                                =      

                                      =      

                                     =      

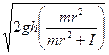
เมื่อคำนวณโดยการใช้กฎการอนุรักษ์พลังงานจะง่ายกว่าการคำนวณโดยใช้แรงและทอร์ค

ทราบหรือไม่ ?  ทำไมความเร่งและความเร็วไม่ขึ้นอยู่กับมวล  ให้นักศึกษาพิจารณาที่ค่าโมเมนต์ความเฉื่อย  ถ้ากำหนดให้    เมื่อ    คือแรงเสียดทานแทนลงในสมการข้างบนจะได้

                          =      

                             =      

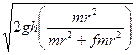
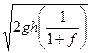
จากสมการที่ได้ค่า    และ    จะไม่ปรากฎ  นั่นคือความเร็วจะไม่ขึ้นกับมวลแต่ขึ้นอยู่กับรูปร่าง  เนื่องจากในสมการมีค่า    ปรากฎอยู่

นักศึกษาตอบได้หรือไม่ว่า  เมื่อปล่อยวงแหวนกับแผ่นจานกลมจากปลายพื้นเอียงพร้อมกันอันไหนจะถึงปลายพื้นเอียงก่อน

 

สรุป

 

นิยามการหมุน

มุม :	การกระจัดเชิงมุม  :
ความเร็วเชิงมุม  :	ความเร่งเชิงมุม :

 

ความสัมพันธ์ระหว่างเชิงเส้นกับเชิงมุม

 

สมการการหมุนจะใช้ได้เมื่อความเร่งเชิงมุม   คงที่

นิยามของทอร์ค                    :        

กฎข้อสองของการหมุน           :        

นิยามของโมเมนต์ความเฉื่อย    :        

ทฤษฎีแกนตั้งฉาก                 :        

ทฤษฎีแกนขนาน                  :        

พลังงานจลน์ในการหมุน          :