 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 14 ของไหล
เนื้อหาประกอบด้วย
14.1 คำจำกัดความของความหนาแน่น และ ความดัน
14.2 ความดันในของไหลที่อยู่นิ่ง
14.3 แรงลอยตัว – กฎของอาร์คีมีดีส (Archimedes’ Principle)
14.4 ของไหลเคลื่อนที่ – สมการแบร์นูลลี (Bernoulli’s Principle)
ของไหล เป็นสารที่สามารถไหลไปมาได้เมื่อมีแรงมากระทำ ในบทนี้จะศึกษาคุณสมบัติของไหล ในเชิงอุดมคติโดยอาศัยกลศาสตร์ดั้งเดิม
14.1 คำจำกัดความของความหนาแน่น และ ความดัน
ความเฉื่อยของของไหลจะแสดงในเทอมของความหนาแน่น แทนที่จะเป็นมวล
ความหนาแน่น : คืออัตราส่วนระหว่างมวลต่อปริมาตร
![]() =
= ![]()
ตัวอย่างที่
14.1
จงหาอัตราส่วนระหว่างมวลของทองคำ ![]() กับมวลของโลก
กับมวลของโลก ![]() เมื่อทองคำเป็นรูปลูกบาศก์ซึ่งมีความยาวด้านละ
เมื่อทองคำเป็นรูปลูกบาศก์ซึ่งมีความยาวด้านละ
![]()
กำหนดให้
ทองคำมีความหนาแน่น ![]()
โลกมีมวล ![]() =
= ![]()
วิธีทำ จาก ![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
ดังนั้น ![]() =
= ![]()
= ![]()
แรงที่กระทำกับของไหลจะแทนด้วยความดันเพื่อความสะดวก
ความดัน : คือแรงที่กระทำต่อหนึ่งหน่วยพื้นที่
![]() =
= ![]()
หน่วยของความดัน
![]() =
= ![]() =
= ![]()
หน่วยที่ได้เรียกว่า พาสคาล (Pascal)
![]() =
= ![]() =
= ![]()
ตัวอย่างที่ 14.2 ทองคำรูปลูกบาศก์ในตัวอย่างที่ 14.1 วางบนพื้น จงหาความดันที่กระทำต่อพื้น
วิธีทำ แรงที่กระทำบนพื้นเป็นแรงเนื่องจากน้ำหนักของทองคำ
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
หน่วยของความดันที่ใช้อยู่ในปัจจุบันมีอยู่หลายหน่วยด้วยกัน แสดงดังตารางข้างล่างนี้
|
Converted to |
1 Pascal 1 Pa |
1 atmosphere 1atm |
1 mmHg 1 Toor |
1 lb/in2 1 psi * |
|
Pa |
1 |
101 kPa |
133 Pa |
6.90 kPa |
|
atm |
|
1 |
|
|
|
mmHg |
|
760 mmHg |
1 |
51.7 mmHg |
|
psi |
|
14.7 psi |
|
1 |
psi = pounds per square inch
14.2ความดันในของไหลที่อยู่นิ่ง
ของไหลอยู่นิ่งจะมีคุณสมบัติ 4 ข้อที่เราต้องทำความเข้าใจ
ก. 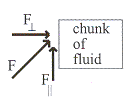 แรงดันจะตั้งฉากกับพื้นที่ผิว ถ้าแรงดันไม่ตั้งฉากหรือทำมุมใด
ๆ กับพื้นที่ผิวของก้อนของไหล ให้แยกองค์ประกอบของแรงในแนวตั้งฉาก
และขนานกับพื้นที่ดังรูปที่ 14.1
ในกรณีนี้แรงที่ตั้งฉากกับพื้นที่ของของเหลวจะทำให้เกิดทอร์คและเกิดการหมุน
อย่างไรก็ตามเนื่องจากของไหลอยู่นิ่งแรงลัพธ์ที่กระทำที่ผิวจะมีค่าเป็นศูนย์
แรงดันจะตั้งฉากกับพื้นที่ผิว ถ้าแรงดันไม่ตั้งฉากหรือทำมุมใด
ๆ กับพื้นที่ผิวของก้อนของไหล ให้แยกองค์ประกอบของแรงในแนวตั้งฉาก
และขนานกับพื้นที่ดังรูปที่ 14.1
ในกรณีนี้แรงที่ตั้งฉากกับพื้นที่ของของเหลวจะทำให้เกิดทอร์คและเกิดการหมุน
อย่างไรก็ตามเนื่องจากของไหลอยู่นิ่งแรงลัพธ์ที่กระทำที่ผิวจะมีค่าเป็นศูนย์
รูปที่ 14.1
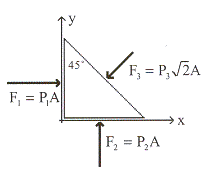 ข.
แรงดันต่อหน่วยพื้นที่มีค่าเท่ากันทุก ๆ จุดบนผิวนั้น
พิจารณาก้อนของเหลวดังรูปที่ 14.2 จากกฎข้อสองของนิวตัน
ข.
แรงดันต่อหน่วยพื้นที่มีค่าเท่ากันทุก ๆ จุดบนผิวนั้น
พิจารณาก้อนของเหลวดังรูปที่ 14.2 จากกฎข้อสองของนิวตัน
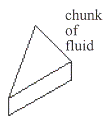
รูปที่ 14.2
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
จากสมการความดัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
นั่นคือทุกด้านของก้อนของเหลวจะมีความดันเท่ากัน ไม่ว่าจะเปลี่ยนรูปร่างของก้อนของเหลวและมุมที่แรงกระทำบนก้อนของเหลว ผลสุดท้ายค่าที่ได้ก็จะมีค่าเท่ากัน สรุปได้ว่าความดันจะค่าเท่ากันในทุกทิศทาง
ค. ความดันในของไหลจะขึ้นอยู่กับความลึกเพียงอย่างเดียว
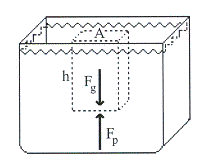 พิจารณาก้อนของเหลวมีพื้นที่หน้าตัด
พิจารณาก้อนของเหลวมีพื้นที่หน้าตัด
![]()
สูง
![]() แรงของก้อนของเหลวคือแรงเนื่องจากน้ำหนัก
แรงของก้อนของเหลวคือแรงเนื่องจากน้ำหนัก![]() แรงที่กระทำที่ด้านล่างของก้อนของเหลวคือแรงดัน
แรงที่กระทำที่ด้านล่างของก้อนของเหลวคือแรงดัน ![]() ส่วนแรงด้านข้างจะหักล้างกันหมด
แสดงดังรูปที่ 14.3 จากกฎข้อสองของนิวตัน
ส่วนแรงด้านข้างจะหักล้างกันหมด
แสดงดังรูปที่ 14.3 จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 14.3 = ![]()
จากสมการความดันและความหนาแน่น
![]() =
= ![]() =
= ![]()
ความดันในของไหลอยู่นิ่ง ![]() =
= ![]()
นั่นคือความดันในกรณีนี้คือน้ำหนักของของเหลว ซึ่งเป็นพื้นฐานที่สำคัญและความดันจะขึ้นอยู่กับความสูงไม่ใช่รูปร่างของของเหลว
ตัวอย่างที่
14.3
ท่อน้ำประปาสำหรับต่อเข้าอาคารสูงมีความดัน ![]() จงคำนวณหาความสูงของอาคารที่สูงที่สุดที่สามารถต่อท่อประปาได้โดยไม่ต้องอาศัยปั๊ม
จงคำนวณหาความสูงของอาคารที่สูงที่สุดที่สามารถต่อท่อประปาได้โดยไม่ต้องอาศัยปั๊ม
วิธีทำ เมื่อไม่คำนึงถึงรูปร่างและขนาดของท่อ ความดันจะขึ้นอยู่กับความสูงเท่านั้น จากสมการความดันในของไหลที่อยู่นิ่ง (เนื่องจากที่ระดับสูงสุดน้ำในท่อจะอยู่นิ่ง)
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
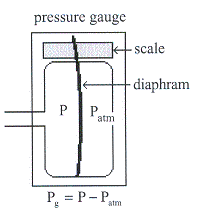 การวัดความดัน
การวัดความดันโดยทั่วไปจะเป็นการเปรียบเทียบ
พิจารณาแผนภาพแสดงเครื่องมือวัดความดันแสดงดังรูปที่ 14.4
ถ้าความดันทั้งสองด้านมีค่าแตกต่างกัน
ความดันด้านที่มากกว่าจะไปดันแผ่นกั้นทำให้เข็มที่ติดอยู่กับแผ่นกั้นเบี่ยงเบนไปทำให้สามารถอ่านค่าได้
การวัดความดัน
การวัดความดันโดยทั่วไปจะเป็นการเปรียบเทียบ
พิจารณาแผนภาพแสดงเครื่องมือวัดความดันแสดงดังรูปที่ 14.4
ถ้าความดันทั้งสองด้านมีค่าแตกต่างกัน
ความดันด้านที่มากกว่าจะไปดันแผ่นกั้นทำให้เข็มที่ติดอยู่กับแผ่นกั้นเบี่ยงเบนไปทำให้สามารถอ่านค่าได้
เครื่องมือวัดความดันจะอ่านค่าได้ศูนย์เมื่อความดันทั้งสองข้างมีค่าเท่ากัน ความดันนี้เรียกว่าความดันสมบูรณ์ (absolute pressure) หรือความดันบรรยากาศ (atmosphere)
ความสัมพันธ์ระหว่างความดันเกจ ![]() และความดันสมบูรณ์
และความดันสมบูรณ์ ![]() คือ
คือ
![]() =
= ![]()
เมื่อ
![]() คือความดันบรรยากาศ
มีค่าเท่ากับ
คือความดันบรรยากาศ
มีค่าเท่ากับ ![]()
รูปที่ 14.4
ตัวอย่างที่ 14.4 จงใช้ความดันสมบูรณ์ เพื่อประมาณค่ามวลของความดันบรรยากาศ
วิธีทำ
จากสมการความดัน ![]() =
= ![]() =
= ![]()
เมื่อ
![]() คือรัศมีของโลก
คือรัศมีของโลก
![]() =
= ![]()
= ![]()
= ![]()
ทำไมเราจึงไม่รู้สึกว่ามีแรงมากระทำ
ง. การประยุกต์การส่งผ่านแรงดันคงที่ จากภายนอกตลอดทั่วของเหลว
(กฎของปาศคาล , Pascal’s Principle)
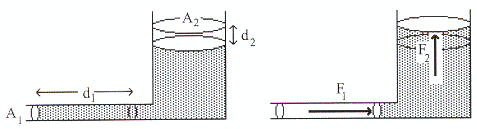
รูปที่ 14.5
จากรูปที่ 14.5 แสดงเครื่องอัดไฮดรอลิก
พิจารณาลูกสูบในกระบอกเล็กเมื่อออกแรง ![]() น้อย ๆ กระทำให้เคลื่อนที่ไปทางขวามือ
จะมีผลทำให้ลูกสูบในกระบอกใหญ่เคลื่อนที่ขึ้น เนื่องจากแรง
น้อย ๆ กระทำให้เคลื่อนที่ไปทางขวามือ
จะมีผลทำให้ลูกสูบในกระบอกใหญ่เคลื่อนที่ขึ้น เนื่องจากแรง ![]() ซึ่งมีค่ามาก
จึงทำให้สามารถยกวัตถุที่มีน้ำหนักมาก ๆ ได้ เมื่อออกแรงน้อย ๆ
ซึ่งมีค่ามาก
จึงทำให้สามารถยกวัตถุที่มีน้ำหนักมาก ๆ ได้ เมื่อออกแรงน้อย ๆ
ของไหลไม่ได้เพิ่มพลังงาน
แต่เกิดจากงานที่ทำบนของไหลเนื่องจากแรง ![]() ซึ่งมีค่าเท่ากับงานที่ใช้ในการยกวัตถุที่มีน้ำหนักมาก
ๆ อันเนื่องมาจากแรง
ซึ่งมีค่าเท่ากับงานที่ใช้ในการยกวัตถุที่มีน้ำหนักมาก
ๆ อันเนื่องมาจากแรง ![]() จากกฎการอนุรักษ์พลังงาน
และสมการของงานจะได้
จากกฎการอนุรักษ์พลังงาน
และสมการของงานจะได้
![]() =
= ![]()
![]()
ปริมาตรของของไหลที่เคลื่อนที่ในกระบอกเล็กจะมีค่าเท่ากับปริมาตรของของไหลที่เคลื่อนที่ในกระบอกใหญ่ จากนั้นนำปริมาตรของของไหลในแต่ละท่อไปหารสมการข้างต้นจะได้
![]() =
= ![]()
![]() =
= ![]()
จากสมการความดัน
![]() =
= ![]()
![]() =
= ![]()
14.3 แรงลอย – กฎของอาร์คีมีดีส (Archimedes’ Principle)
ทำไมวัตถุบางชนิดจมบางชนิดลอย เนื่องจากของไหลออกแรงกระทำต่อวัตถุ แรงนี้เรียกว่า แรงพยุง (buoyant force) เมื่อแรงพยุงคือผลต่างของความดัน เป็นการเปรียบเทียบความดันระหว่างด้านบนของวัตถุ กับความดันด้านล่างของวัตถุ แรงพยุงที่กระทำต่อวัตถุแสดงดังรูปที่ 14.5
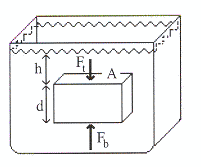
![]() =
= ![]()
อาศัยความสัมพันธ์ระหว่างแรงกับความดัน เมื่อความดันขึ้นอยู่กับความลึกในของเหลว
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
![]()
นั่นคือแรงพยุงเป็นผลมาจากความหนาแน่นของ รูปที่ 14.5 ของเหลว และปริมาตรส่วนที่จมของวัตถุ ซึ่งมีค่าเท่ากับมวลของของเหลวที่ถูกแทนที่ด้วยวัตถุ
กฎของอาร์คีมีดีส “แรงพยุงจะมีค่าเท่ากับน้ำหนักของของเหลวที่ถูกแทนที่ด้วยวัตถุ” สามารถเขียนอยู่ในรูปสมการทางคณิตศาสตร์ได้ดังนี้
![]() =
= ![]() (
(
![]() คือมวลของของเหลว
)
คือมวลของของเหลว
)
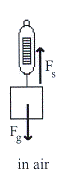 ตัวอย่างที่
14.5
กล่องโลหะมวล
ตัวอย่างที่
14.5
กล่องโลหะมวล ![]() กรัม
เมื่อชั่งในอากาศ แต่อ่านได้
กรัม
เมื่อชั่งในอากาศ แต่อ่านได้ ![]() กรัมเมื่อช่งในน้ำ จงหาความหนาแน่นของกล่องโลหะนี้
กรัมเมื่อช่งในน้ำ จงหาความหนาแน่นของกล่องโลหะนี้
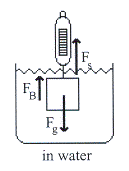
รูปที่ 14.6 ก. รูปที่ 14.6 ข.
วิธีทำ เมื่อชั่งในอากาศจะมีแรงเนื่องจากน้ำหนักเพียงอย่างเดียว ซึ่งแรงนี้จะไปกระทำต่อตาชั่ง ดังรูปที่ 14.6 ก. แต่เมื่อนำไปชั่งในน้ำจะมีแรงพยุงเพิ่มเข้ามาดังรูปที่ 14.6 ข. ทำให้ตาชั่งอ่านค่าได้น้อยลง
จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
จากกฎของอาร์คีมีดีส
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
จากสมการความหนาแน่นเพื่อหาปริมาตรของกล่องโลหะ
![]() =
= ![]()
![]() =
= ![]()
จากสมการความหนาแน่นเพื่อหาความหนาแน่นของกล่องโลหะ
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
แรงพยุงเป็นแรงชนิดหนึ่งดังนั้นสามารจัดการหรือคำนวณได้เหมือนแรงชนิดอื่น ๆ เช่น แรงเสียดทาน แรงจากภายนอก แรงโน้มถ่วง เป็นต้น
ตัวอย่างที่ 14.6 จงคำนวณหาปริมาตรส่วนที่จมต่อปริมาตรทั้งหมดของก้อนน้ำแข็งที่ลอยอยู่ในน้ำดังรูปที่ 14.7
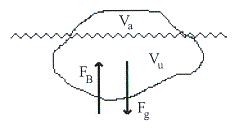 วิธีทำ
แรงที่กระทำต่อวัตถุคือแรงเนื่องจากน้ำหนัก
วิธีทำ
แรงที่กระทำต่อวัตถุคือแรงเนื่องจากน้ำหนัก ![]() และแรงพยุง
และแรงพยุง ![]()
จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
จากกฎของอาร์คีมีดีส โดยอาศัยความจริงที่ว่า รูปที่ 14.7 ปริมาตรส่วนที่จมของวัตถุจะเข้าไปแทนที่น้ำ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เมื่อ ![]() คือมวลของน้ำที่ถูกแทนที่
;
คือมวลของน้ำที่ถูกแทนที่
;![]() คือปริมาตรส่วนที่ลอย ;
คือปริมาตรส่วนที่ลอย ;![]() คือปริมาตรส่วนที่จมจากนิยามของความหนาแน่น
คือปริมาตรส่วนที่จมจากนิยามของความหนาแน่น
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ก้อนน้ำแข็งจะลอยเหนือน้ำ
![]() =
= ![]()
= ![]()
14.4 ของไหลเคลื่อนที่ - สมการแบร์นูลลี (Bernoulli’s Principle)
สมการแบร์นูลลี ความในของไหลเคลื่อนที่จะมีค่าน้อยกว่าความดันในของไหลที่อยู่นิ่ง สังเกตได้จากเมื่อใช้มือจับเศษกระดาษชิ้นยาว ๆ แล้วเป่า จะเห็นว่ากระดาษจะยกตัวขึ้น
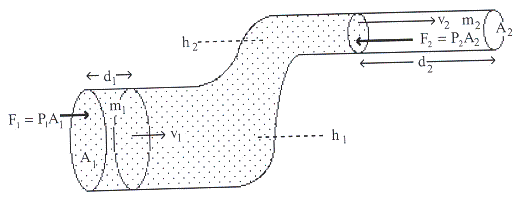
รูปที่ 14.8
เมื่อของไหลเคลื่อนที่จะเป็นการง่ายเมื่อพิจารณาในรูปของพลังงาน
แทนพิจารณาในรูปของแรง พิจารณาของไหลส่วนเล็ก ๆ ในท่อ
ซึ่งเคลื่อนที่ไปทางขวามือเมื่อขนาดของท่อมีขนาดเล็กลงแสดงดังรูปที่ 14.8
ให้ของไหลที่ปลายด้านล่างเคลื่อนที่ได้ระยะทาง ![]() ทำให้ของไหลในท่อด้านบนเคลื่อนที่ได้ระยะทาง
ทำให้ของไหลในท่อด้านบนเคลื่อนที่ได้ระยะทาง
![]() เป็นของไหลที่อัดไม่ได้
มวลของของไหลที่เคลื่อนที่อยู่ภายในท่อด้านบนและด้านล่างจะมีค่าเท่ากัน
จากนิยามของความหนาแน่น
เป็นของไหลที่อัดไม่ได้
มวลของของไหลที่เคลื่อนที่อยู่ภายในท่อด้านบนและด้านล่างจะมีค่าเท่ากัน
จากนิยามของความหนาแน่น
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
เวลาที่ของไหลใช้ในการเคลื่อนที่มีค่าเท่ากัน เมื่อนำมาหารสมการด้านบนทั้งสองข้างจะได้
![]() =
= ![]()
![]() =
= ![]()
สมการที่ได้เรียกว่าสมการแห่งความต่อเนื่อง (equation of continuity)
แรงดันที่ท่อด้านล่าง แรงดันที่ท่อด้านบน และแรงโน้มถ่วง แรงทั้งหมดจะทำให้เกิดงานเนื่องจากของไหล จากทฤษฎีของงาน – พลังงาน งานทั้งหมดที่เกิดจากการเคลื่อนที่ของของไหลส่วนเล็ก ๆ ที่พิจารณา จะมีค่าเท่ากับการเปลี่ยนแปลงพลังงานจลน์ของมวลที่เคลื่อนที่
![]() =
= ![]()
จากนิยามของความดันและความหนาแน่น
![]() =
=
![]()
เมื่อปริมาตรของไหลส่วนที่เคลื่อนที่ในท่อล่างกับท่อบนมีค่าเท่ากัน
![]() =
= ![]()
![]() =
= ![]()
สมการที่ได้เรียกว่าสมการแบร์นูลลี นั่นคือ
![]() = ค่าคงที่
= ค่าคงที่
ตัวอย่างที่
14.7
จงคำนวณหาความเร็วของน้ำที่ไหลผ่านรอยรั่วที่ฐานของเขื่อนกั้นน้ำ
ถ้าระดับน้ำในเขื่อนสูง ![]()
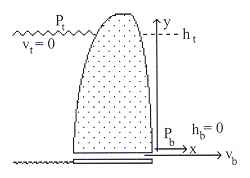 วิธีทำ จากรูปที่
14.9 กำหนดให้ฐานเขื่อนอยู่ที่ตำแหน่ง
วิธีทำ จากรูปที่
14.9 กำหนดให้ฐานเขื่อนอยู่ที่ตำแหน่ง ![]() น้ำไหลออกจากรอยรั่วที่ฐานเขื่อน
และกำหนดให้น้ำบริเวณเหนือเขื่อนมีความเร็วเป็นศูนย์
(เนื่องจากรอยรั่วมีขนาดเล็กมากเมื่อเทียบกับบริเวณเหนือเขื่อน)
น้ำไหลออกจากรอยรั่วที่ฐานเขื่อน
และกำหนดให้น้ำบริเวณเหนือเขื่อนมีความเร็วเป็นศูนย์
(เนื่องจากรอยรั่วมีขนาดเล็กมากเมื่อเทียบกับบริเวณเหนือเขื่อน)
จากสมการแบร์นูลลี
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 14.9
แต่ความดันบรรยากาศเหนือเขื่อนจะมีค่าเท่ากับความดันบรรยากาศที่ฐานเขื่อนคือ
![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
หลัการนี้ใช้คำนวณได้กับรอยรั่วทั่ว ๆ ไปที่มีลักษณะเช่นนี้
ตัวอย่างที่ 14.8 จงหาความเร็วของอากาศเหนือลูกปิงปองที่ลอยอยู่ดังรูปที่ 14.10
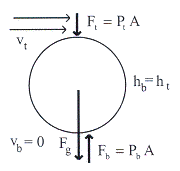 วิธีทำ ให้ความแตกต่างระหว่างด้านบนกับด้านล่างไม่มีผลต่อความสูงของลูกปิงปอง
เนื่องจากลูกปิงปองมีขนาดเล็ก ดังนั้นผลต่างระหว่างความสูงจึงมีค่าน้อยมากนั่นคือ
วิธีทำ ให้ความแตกต่างระหว่างด้านบนกับด้านล่างไม่มีผลต่อความสูงของลูกปิงปอง
เนื่องจากลูกปิงปองมีขนาดเล็ก ดังนั้นผลต่างระหว่างความสูงจึงมีค่าน้อยมากนั่นคือ
![]()
จากสมการของแบร์นูลลี
![]() =
= ![]()
เมื่อ
![]()
![]() =
= ![]()
รูปที่ 14.10 กำหนดให้ความเร็วด้านล่างของลูกปิงปองมีค่าเข้าใกล้ศุนย์
![]() =
= ![]()
![]() =
= ![]()
ความแตกต่างของความดันสามารถหาได้จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
หารสมการทั้งสองข้างด้วยพื้นที่หน้าตัด
![]() ของลูกปิงปอง
จากนั้นใช้สมการความดัน
ของลูกปิงปอง
จากนั้นใช้สมการความดัน
![]() =
= ![]()
![]() =
= ![]()
แทนค่าสมการ
![]() จะได้
จะได้
![]() =
= ![]()
![]() =
= 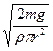
กำหนดให้
![]() ;
; ![]() และ
และ
![]()
![]() =
= 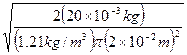
= ![]()
สรุป
ความหนาแน่น
: ![]()
ความดัน
: ![]()
ความดันในของไหลที่อยู่นิ่ง
: ![]()
กฎของอาร์คิมีดีส
: ![]()
สมการการไหลต่อเนื่อง
: ![]()
สมการแบร์นูลลี
: ![]()