 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 12 สมดุล
ในบทนี้จะศึกษาเกี่ยวกับวัตถุที่อยู่นิ่ง หรือที่เรียกว่าอยู่ในสภาวะสมดุลสถิต (static equilibrium) ซึ่งมีความสำคัญมากในการออกแบบอาคาร สะพาน หรือโครงสร้างต่าง ๆ
เมื่อวัตถุอยู่ในสภาวะสมดุลสถิตวัตถุจะไม่มีความเร่งเชิงเส้น และความเร่งเชิงมุม จากกฎของสองของนิวตันเมื่อวัตถุมีการเคลื่อนที่ และสมการการหมุน
![]() =
= ![]()
![]()
![]() =
= ![]()
และ
![]() =
= ![]()
![]()
![]() =
= ![]()
นั่นคือแรงลัพธ์และทอร์คลัพธ์ที่กระทำต่อวัตถุจะมีค่าเท่ากับศูนย์
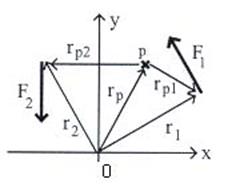 ทอร์คจะขึ้นอยู่กับจุดหมุนที่เราเลือก
พิจารณารูปที่ 12.1 เมื่อวัตถุสมดุลภายใต้แรงทั้งสอง
ผลรวมของทอร์คเมื่อเทียบกับจุดกำเนิด
ทอร์คจะขึ้นอยู่กับจุดหมุนที่เราเลือก
พิจารณารูปที่ 12.1 เมื่อวัตถุสมดุลภายใต้แรงทั้งสอง
ผลรวมของทอร์คเมื่อเทียบกับจุดกำเนิด ![]() จะมีค่าเท่ากับศูนย์
ในนำนองเดียวกันที่จุด
จะมีค่าเท่ากับศูนย์
ในนำนองเดียวกันที่จุด ![]() ถ้าระบบสมดุลผลรวมของทอร์ครอบจุด
ถ้าระบบสมดุลผลรวมของทอร์ครอบจุด ![]() จะมีค่าเท่ากับศูนย์เช่นกัน
จะมีค่าเท่ากับศูนย์เช่นกัน
ทอร์ครอบจุด
![]() คือ
คือ
![]() =
= ![]()
เวกเตอร์ตำแหน่งเขียนได้ดังนี้
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 12.1
ดังนั้นทอร์ครอบจุด
![]() สามารถเขียนใหม่ได้เป็น
สามารถเขียนใหม่ได้เป็น
![]() =
= ![]()
อาศัยกฎการกระจาย
จัดเทอมใหม่
![]() =
= ![]()
= ![]()
เทอมแรกที่ได้เป็นทอร์ครอบจุดกำเนิด ส่วนเทอมที่สองค่าในวงเล็บเป็นทอร์คที่เกิดจากแรงรวมทั้งหมด
![]() =
= ![]()
เนื่องจากทอร์ครอบจุดกำเนิดเท่ากับศูนย์ และทอร์คที่เกิดจากแรงลัพธ์มีค่าเท่ากับศูยน์วัตถุจึงสมดุลล
ตัวอย่างที่
12.1
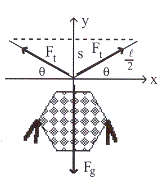
โคมไฟหนัก ![]() แขวนที่จุดกึ่งกลางของเชือกซึ่งยาว
แขวนที่จุดกึ่งกลางของเชือกซึ่งยาว
![]() ทำให้เชือกหย่นลงมา
ทำให้เชือกหย่นลงมา
![]() จากแนวระดับดังรูปที่
12.2 จงหาแรงตึงเชือก
จากแนวระดับดังรูปที่
12.2 จงหาแรงตึงเชือก
วิธีทำ มุมที่แรงตึงเชือกกระทำกับแนวระดับ คำนวณได้จาก
![]() =
= ![]() =
= ![]()
ให้ ![]() คือระยะที่เชือกหย่อนจากแนวระดับ
คือระยะที่เชือกหย่อนจากแนวระดับ
![]() คือความยาวเชือก
คือความยาวเชือก
![]() =
= ![]()
= ![]()
รูปที่ 12.2
แต่โคมไฟแขวนอยู่ที่จุดกึ่งกลางของเชือก ทำให้มุมและแรงตึงเชือกทั้งสองด้านมีค่าเท่ากัน อาศัยกฎข้อสองของนิวตันพิจารณาที่ตำแหน่งเชือกติดกับโคมไฟ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
ตังอย่างที่
12.2
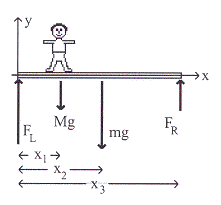
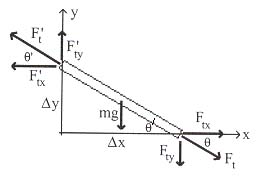
ไม้กระดานยาว ![]() มีมวล
มีมวล
![]() ที่ปลายทั้งสองด้านมีเสาค้ำอยู่
ชายคนหนึ่งมีมวล
ที่ปลายทั้งสองด้านมีเสาค้ำอยู่
ชายคนหนึ่งมีมวล ![]() ยืนห่างจากปลายไม้กระดานทางซ้ายมือเป็นระยะ
ยืนห่างจากปลายไม้กระดานทางซ้ายมือเป็นระยะ
![]() ดังรูปที่
12.3 จงหาแรงที่เสาแต่ละต้น
ดังรูปที่
12.3 จงหาแรงที่เสาแต่ละต้น
 วิธีทำ
การเลือกจุดหมุนให้เลือกจุดที่ไม่ทราบค่า จุดใดจุดหนึ่งให้เป็นจุดหมุน
เพื่อให้ง่ายต่อการคำนวณเนื่องจากจะทำให้ค่าทอร์คเป็นศูนย์
วิธีทำ
การเลือกจุดหมุนให้เลือกจุดที่ไม่ทราบค่า จุดใดจุดหนึ่งให้เป็นจุดหมุน
เพื่อให้ง่ายต่อการคำนวณเนื่องจากจะทำให้ค่าทอร์คเป็นศูนย์
จากกฎการหมุน
พิจารณาที่ไม้กระดาน เมื่อให้จุดที่มีแรง ![]() ผ่านเป็นจุดหมุน
และกำหนดให้ทอร์คทวนเข็มนาฬิกามีค่าเป็นบวก
ผ่านเป็นจุดหมุน
และกำหนดให้ทอร์คทวนเข็มนาฬิกามีค่าเป็นบวก
รูปที่ 12.3
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าต่าง ๆ ลงในสมการ
![]() =
= ![]()
= ![]()
จากกฎข้อสองของนิวตัน
![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
ตัวอย่างที่
13.3
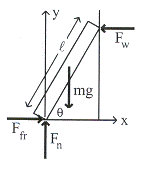
หนังสือมวล ![]() โดยวางเอียงกับชั้นวางหนังสือลื่น
โดยวางทำมุม
โดยวางเอียงกับชั้นวางหนังสือลื่น
โดยวางทำมุม ![]() กับพื้นดังรูปที่
12.4 จงหาแรงต่าง ที่กระทำต่อหนังสือแล้วทำให้หนังสือสมดุล
กับพื้นดังรูปที่
12.4 จงหาแรงต่าง ที่กระทำต่อหนังสือแล้วทำให้หนังสือสมดุล
 วิธีทำ
จะไม่มีแรงเสียดทานระหว่างหนังสือกับชั้นวางเนื่องจากเป็นชั้นลื่น
พิจารณาแรงต่าง ๆ ที่กระทำต่อหนังสือจะได้ว่า
วิธีทำ
จะไม่มีแรงเสียดทานระหว่างหนังสือกับชั้นวางเนื่องจากเป็นชั้นลื่น
พิจารณาแรงต่าง ๆ ที่กระทำต่อหนังสือจะได้ว่า
![]() =
= ![]() =
= ![]()
จากกฎข้อสองของนิวตัน และการหมุน โดยพิจารณาดังรูปที่ 12.4 พิจารณาการเลื่อนตำแหน่ง
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() ……………(1)
……………(1)
![]() =
= ![]()
รูปที่
12.4 ![]() =
= ![]()
![]() =
= ![]()
= ![]()
พิจารณาการหมุน กำหนดให้ที่พื้นเป็นจุดหมุน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
แทนค่า
![]() ลงในสมการที่
(1)
ลงในสมการที่
(1)
![]() =
= ![]()
ตัวอย่างที่
13.4
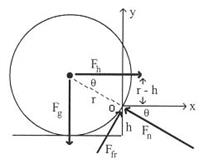
ล้อจักรยานเสือภูเขารัศมี ![]() รับน้ำหนัก
รับน้ำหนัก ![]() จงหาแรงที่น้อยที่สุดที่กระทำผ่านแกนของล้อในแนวราบ
จงหาแรงที่น้อยที่สุดที่กระทำผ่านแกนของล้อในแนวราบ
![]() แล้วทำให้ล้อจักรยานเสือภูเขาเคลื่อนที่ผ่านขอบถนนซึ่งสูง
แล้วทำให้ล้อจักรยานเสือภูเขาเคลื่อนที่ผ่านขอบถนนซึ่งสูง
![]() ได้
ดังรูปที่ 12.5
ได้
ดังรูปที่ 12.5
 วิธีทำ
หาแรงที่กระทำต่อล้อจักรยานเสือภูเขา ได้แก่แรงเนื่องจากน้ำหนัก
วิธีทำ
หาแรงที่กระทำต่อล้อจักรยานเสือภูเขา ได้แก่แรงเนื่องจากน้ำหนัก ![]() แรงในแนวราบ
แรงในแนวราบ ![]() ซึ่งเป็นแรงเนื่องจากรถ
แรงปฎิกริยา
ซึ่งเป็นแรงเนื่องจากรถ
แรงปฎิกริยา ![]() เนื่องจากขอบถนนกระทำกับล้อรถจักรยานโดยแรงนี้จะผ่านจุดศูนย์กลางของล้อรถ
และแรงเสียดทาน
เนื่องจากขอบถนนกระทำกับล้อรถจักรยานโดยแรงนี้จะผ่านจุดศูนย์กลางของล้อรถ
และแรงเสียดทาน![]()
![]() เนื่องจากขอบถนน
ส่วนแรงปฎิกริยาที่พื้นกระทำต่อล้อรถจะมีค่าเป็นศูนย์
เนื่องจากล้อรถยกตัวจากพื้นขณะที่จะผ่านขอบถนน มุมที่แรงปฎิกริยากระทำกับแนวราบสามารถคำนวณได้จากกฎของ
เนื่องจากขอบถนน
ส่วนแรงปฎิกริยาที่พื้นกระทำต่อล้อรถจะมีค่าเป็นศูนย์
เนื่องจากล้อรถยกตัวจากพื้นขณะที่จะผ่านขอบถนน มุมที่แรงปฎิกริยากระทำกับแนวราบสามารถคำนวณได้จากกฎของ
![]()
รูปที่
12.5 ![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ใช้ขอบถนนเป็นจุดหมุนเนื่องจากเราไม่ทราบแรงปฎิกริยา จากสมการการหมุน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
= ![]()
 ตัวอย่างที่
13.5
จงคำนวณหารูปร่างของสายเคเบิลที่รองรับสะพานมวล
ตัวอย่างที่
13.5
จงคำนวณหารูปร่างของสายเคเบิลที่รองรับสะพานมวล ![]() เมื่อระยะห่างระหว่างตอม่อสะพานในแนวระดับยาว
เมื่อระยะห่างระหว่างตอม่อสะพานในแนวระดับยาว
![]() ดังรูปที่
12.6
ดังรูปที่
12.6
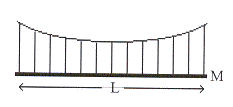
รูปที่ 12.6 รูปที่ 12.7
วิธีทำ
แรงที่กระทำต่อสายเคเบิ้ลส่วนเล็ก ๆ
ประกอบด้วยแรงตึงเชือกที่กระทำต่อส่วนบนของเส้นเชือก ![]() แรงตึงเชือกที่ส่วนล่างของเส้นเชือก
แรงตึงเชือกที่ส่วนล่างของเส้นเชือก
![]() และน้ำหนักของถนนส่วนเล็ก
ๆ ซึ่งอยู่ใต้สายเคเบิ้ลส่วนเล็ก ๆ ที่เราพิจารณาดังรูปที่ 12.7
และน้ำหนักของถนนส่วนเล็ก
ๆ ซึ่งอยู่ใต้สายเคเบิ้ลส่วนเล็ก ๆ ที่เราพิจารณาดังรูปที่ 12.7
พิจารณาส่วนเล็ก ๆ จากกฎข้อสองของนิวตัน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
และ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แต่สัดส่วนของน้ำหนักส่วนเล็ก ๆ เทียบกับน้ำหนักทั้งหมด จะมีค่าเท่ากับระยะในแนวราบเล็ก ๆ เทียบกับระยะทางในแนวราบทั้งหมด
![]() =
= ![]()
![]() =
= ![]()
จากสมการในแนวแกน
![]() สามารถเขียนใหม่ได้เป็น
สามารถเขียนใหม่ได้เป็น
![]() =
= ![]()
จะได้ ![]() =
= ![]() ………..
(1)
………..
(1)
จากรูปที่ 12.7 จะได้มุมแสดงความสัมพันธ์ของแรงตึงเชือกคือ
![]() =
= ![]()
และ ![]() =
= ![]()
เนื่องจากองค์ประกอบในแนวแกน ![]() ของแรงตึงเชือกไม่มีการเปลี่ยนแปลง
ดังนั้นการเปลี่ยนแปลงของมุมคือ
ของแรงตึงเชือกไม่มีการเปลี่ยนแปลง
ดังนั้นการเปลี่ยนแปลงของมุมคือ
![]() =
= ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่าลงในสมการแนวแกน
![]() (สมการที่
1)
(สมการที่
1)
![]() =
= ![]()
![]() =
= ![]()
Take
limit ให้ ![]() จะได้
จะได้
![]() =
= ![]() =
= ![]() ………
(2)
………
(2)
เมื่อค่า
![]() สามารถเขียนอยู่ในรูปของเทอม
สามารถเขียนอยู่ในรูปของเทอม
![]() และ
และ ![]() ได้ ดังนั้น
ได้ ดังนั้น
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
แทนค่ามุม
![]() ลงในสมการที่
(2)
ลงในสมการที่
(2)
![]() =
= ![]()
![]() =
= ![]()
สมการที่ได้ค่าทางขวามือจะเป็นค่าคงที่ ดังนั้นคำตอบของสมการคือ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
จะได้เป็นรูปพาลาโบล่า ซึ่งคำนวณมาจากกฎการเคลื่อนที่ของนิวตันนั่นเอง
สรุป
สมดุล
: ![]() และ
และ ![]()