 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 3 การเคลื่อนที่ใน 2 มิติและ 3 มิติ
เนื้อหาประกอบด้วย
3.1 คำจำกัดความของตำแหน่ง การกระจัด ความเร็วและความเร่ง
3.2 การเคลื่อนที่แบบโปรเจคไตด์
3.3 การเคลื่อนที่แบบวงกลมสม่ำเสมอ
การเคลื่อนที่ใน 2 มิติและ 3 มิติ วัตถุไม่จำเป็นต้องเคลื่อนที่เป็นเส้นตรงเสมอไป ในบทนี้จะอธิบายถึงความหมายของคำต่าง ๆ เพื่อให้เกิดความเข้าใจเกี่ยวกับ ตำแหน่ง การกระจัด ความเร็ว ความเร่ง โดยอาศัยเงื่อนไขของเวกเตอร์เพื่ออธิบายปรากฎการต่าง ๆ ที่เกิดขึ้น
3.1 คำจำกัดความตำแหน่ง การกระจัด ความเร็วและความเร่ง
คำจำกัดความเกี่ยวกับตำแหน่ง การกระจัด ความเร็วและความเร่ง ดังได้กล่าวในบทที่ 1 ในบทนี้จะอธิบายในรูปของเวกเตอร์
ตำแหน่ง : บริเวณที่ตั้งของวัตถุซึ่งสัมพันธ์กับระบบพิกัดฉาก
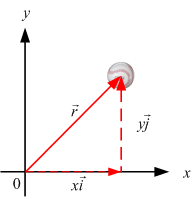
จากรูปที่ 3.1 แสดงตำแหน่งของวัตถุเมื่อเขียนอยู่ในรูปของเวกเตอร์
![]() =
= ![]()
รูปที่ 3.1 แสดงตำแหน่งของวัตถุ
การกระจัด : เกิดขึ้นเมื่อมีการเปลี่ยนแปลงตำแหน่ง
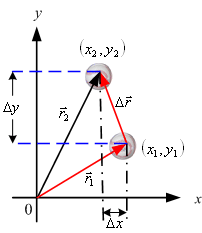
จากรูปที่ 3.2 การกระจัดเมื่อเขียนอยู่ในรูปของเวกเตอร์
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
รูปที่ 3.2 แสดงการเปลี่ยนตำแหน่งของวัตถุ
ความเร็วเฉลี่ย : คือการกระจัดที่เปลี่ยนไปในช่วงเวลาที่วัตถุเคลื่อนที่
เขียนในรูปสมการทางคณิตศาสตร์
![]() =
= ![]()
เมื่อแทนค่า
![]() จากตอนต้นรูปที่ 3.2 จะได้
จากตอนต้นรูปที่ 3.2 จะได้
![]() =
= ![]() =
= ![]()
= ![]()
อัตราเร็วคือขาดของความเร็ว
เขียนในรูปสมการทางคณิตศาสตร์
![]() =
= ![]() =
= ![]()
ตัวอย่างที่
3.1 นักศึกษาคนหนึ่งเริ่มออกเดินทางจากหอพักไปทางทิศเหนือเป็นระยะทาง
![]() จากนั้นเดินไปทางทิศตะวันออกเป็นระยะทาง
จากนั้นเดินไปทางทิศตะวันออกเป็นระยะทาง
![]() โดยใช้เวลาทั้งหมด
โดยใช้เวลาทั้งหมด ![]() จงคำนวณหา
จงคำนวณหา
ก. ตำแหน่งเริ่มต้น ข. ตำแหน่งสุดท้าย
ค. การกระจัด ง. ความเร็วเฉลี่ย
จ. อัตราเร็วเฉลี่ย
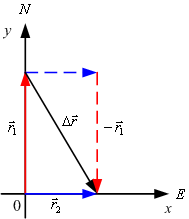
วิธีทำ จากรูปที่ 3.3 จะได้
ก. ![]() =
= ![]()
ข. ![]() =
= ![]()
ค. ![]() =
= ![]()
= ![]()
ง. ![]() =
= ![]()
= ![]()
= ![]()
รูปที่ 3.3
จ. ![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
ความเร่งเฉลี่ย : คือความเร็วของวัตุที่เปลี่ยนไปเทียบกับช่วงเวลาที่เปลี่ยนไปในการเคลื่อนที่
เขียนในรูปสมการทางคณิตศาสตร์
![]() =
= ![]()
![]()
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
ในกรณี 3 มิติพิจารณาทำนองเดียวกับ 2 มิติ เพียงแต่เพิ่มส่วนประกอบในแนวแกน ![]() เข้าไป
เข้าไป
ตำแหน่ง : ![]()
การกระจัด : ![]()
ความเร็วเฉลี่ย : ![]()
อัตราเร็ว : ![]()
ความเร่งเฉลี่ย : ![]()
ตัวอย่างที่
3.2 ฟุตบอลมีความเร็ว
![]() ในหน่วย
ในหน่วย ![]() ต่อมาความเร็วเปลี่ยนเป็น
ต่อมาความเร็วเปลี่ยนเป็น ![]() ภายในเวลา
ภายในเวลา ![]() จงหา
จงหา
ก. ความเร่งเฉลี่ยในรูปของเวกเตอร์
ข. ขนาดของความเร่งเฉลี่ย
วิธีทำ ก. ![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
ข. ![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
เพื่อความสะดวกในการคำนวณเราสามารถใช้แคลลูลัสเข้าช่วยโดยการเปลี่ยน ![]() เป็น
เป็น
![]() พิจารณาดังนี้
พิจารณาดังนี้
จากนิยามของตำแหน่ง : ![]()
จากนิยามของการกระจัด : ![]()
จากนิยามของความเร็ว : ![]()
จากนิยามของอัตราเร็ว : ![]()
จากนิยามของความเร่ง : ![]()
ตัวอย่างที่
3.3 จงหาความเร็วขณะใดขณะหนึ่งของเข็มยาวนาฬิกาซึ่งยาว
![]() ดัรูปที่ 3.4
ดัรูปที่ 3.4
วิธีทำ จากรูปที่
3.4 เมื่อตั้งระบบแกนพิกัดฉากดังรูป พิจารณาเข็มนาฬิกาก่อนถึงตำแหน่งสูงสุดเล็กน้อย
โดยทำมุม ![]() น้อย ๆ ก่อนถึงแกน
น้อย ๆ ก่อนถึงแกน ![]() จะได้ว่า
จะได้ว่า

![]() =
= ![]()
จากนั้นพิจารณาเข็มนาฬิกา
ภายหลังผ่านจุดสูงสุดเล็กน้อย โดยทำมุม ![]() น้อย ๆ กับแกน
น้อย ๆ กับแกน
![]() ไปทางขวามือ ดังนั้นจะได้ว่า
ไปทางขวามือ ดังนั้นจะได้ว่า
![]() =
= ![]()
เมื่อ ![]() คือความยาวของเข็มนาฬิกา
คือความยาวของเข็มนาฬิกา
รูปที่ 3.4
จากคำกำจัดความของการกระจัด
![]() =
= ![]()
= ![]()
= ![]()
พิจารณา
![]() น้อยมาก ๆ จะได้ว่า
น้อยมาก ๆ จะได้ว่า ![]() จะได้
จะได้
![]() =
= ![]() =
= ![]()
จากนิยามของความเร็ว
![]() =
= ![]() =
= ![]()
ให้
![]() ; ความเร็วขณะใดขณะหนึ่งเขียนได้เป็น
; ความเร็วขณะใดขณะหนึ่งเขียนได้เป็น
![]() =
= ![]()
เมื่อ
![]() คือระยะทางเชิงมุมของการหมุนเป็นค่าคงที่
เมื่อหมุนครบ 1 รอบจะได้
คือระยะทางเชิงมุมของการหมุนเป็นค่าคงที่
เมื่อหมุนครบ 1 รอบจะได้
![]() =
= ![]() =
= ![]()
แทนค่าในสมการ
![]() =
= ![]()
= ![]()
ตัวอย่างที่ 3.4 จากข้อ 3.3 จงหาความเร่งของปลายเข็มนาฬิกาดังรูปที่ 3.5
รูปที่ 3.5 รูปที่ 3.6
วิธีทำ เวกเตอร์ความเร็วคือเส้นสัมผัสวงกลมที่
จุดใด ๆ พิจารณาความเร็วเริ่มต้น ![]() และความเร็วสุดท้าย
และความเร็วสุดท้าย
![]() ซึ่งทำมุม
ซึ่งทำมุม ![]() กับแนวระดับดังรูปที่ 3.5
เพื่อความสะดวกในการคำนวณเราสามารถแยก
กับแนวระดับดังรูปที่ 3.5
เพื่อความสะดวกในการคำนวณเราสามารถแยก ![]() ให้อยู่ในองค์ประกอบตามแกน
ให้อยู่ในองค์ประกอบตามแกน ![]() และ
และ ![]() ได้ดังรูปที่ 3.6
ได้ดังรูปที่ 3.6
![]() =
= ![]() และ
และ
![]() =
= ![]()
เมื่อ
![]() คืออัตราเร็วของปลายเข็มทั้งสอง
คืออัตราเร็วของปลายเข็มทั้งสอง
พิจารณาการเปลี่ยนแปลงความเร็ว
![]() =
= ![]()
= ![]()
= ![]()
ให้
![]() มีค่าน้อยมาก ๆ จะได้
มีค่าน้อยมาก ๆ จะได้
![]()
จะได้
![]() =
= ![]() =
= ![]()
จากนิยามของความเร่ง
; ![]() =
= ![]() =
= ![]()
ให้
![]() จะได้ความเร่งขณะใดขณะหนึ่งคือ
จะได้ความเร่งขณะใดขณะหนึ่งคือ
![]() =
= ![]()
= ![]()
= ![]()
จากตัวอย่างที่ 3.3 และ 3.4 จะสังเกตุเห็นว่าขณะที่อัตราเร็วคงที่ แต่ทิศทางเปลี่ยนแปลง ความเร่งก็มีค่าคงที่ แต่มีทิศเข้าสู่ศูนย์กลาง
ตัวอย่างที่
3.5 แมลงตัวหนึ่งบินอยู่ที่ตำแหน่ง
![]() ซึ่งเป็นฟังก์ชั่นของเวลา จงหา
ซึ่งเป็นฟังก์ชั่นของเวลา จงหา
ก. ความเร็วเป็นฟังก์ชั่นของเวลา
ข. ความเร่งเป็นฟังก์ชั่นของเวลา
วิธีทำ ก. ![]() =
= ![]() =
= ![]()
= ![]()
ข. ![]() =
= ![]() =
= ![]()
= ![]()
3.2 การเคลื่อนที่แบบโปรเจกไตล์
จากกฎการเคลื่อนที่ในแนวดิ่งเราสามารถนำมาประยุกต์ใช้ในการเคลื่อนที่แบบโปรเจกไตล์
ซึ่งเป็นการเคลื่อนที่ใน 2
มิติ การเคลื่อนที่แบบนี้จะได้ความเร่ง ![]() พิจารณาวัตถุเคลื่อนที่ด้วยความเร็ว
พิจารณาวัตถุเคลื่อนที่ด้วยความเร็ว
![]() ทิศดังรูปที่ 3.7 จากนิยามความเร็วและความเร่ง
สามารถนำมาหาสมการการเคลื่อนที่แบบโปรเจกไตล์ได้ดังนี้
ทิศดังรูปที่ 3.7 จากนิยามความเร็วและความเร่ง
สามารถนำมาหาสมการการเคลื่อนที่แบบโปรเจกไตล์ได้ดังนี้
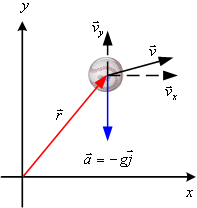
จากนิยามความเร่ง
![]() =
= ![]()
![]() =
= ![]()
= ![]()
รูปที่ 3.7
จากสมการเวกเตอร์ที่ได้ เมื่อเทียบสัมประสิทธิองค์ประกอบของเวกเตอร์ในแต่ละแกน สามารถแยกเขียนได้เป็น 2 สมการคือ
![]() =
= ![]()
และ ![]() =
= ![]()
นั่นคือการเคลื่อนที่แบบโปรเจกไตล์ความเร่งจะมีค่าคงที่
การเคลื่อนที่แบบนี้สามารถแยกพิจารณาในแต่ละแกนได้โดยอาศัยเงื่อนไขที่ว่าความเร่งในแนวแกน
![]() จะมีค่าเป็นศูนย์
จะมีความเร่งเฉพาะแกน
จะมีค่าเป็นศูนย์
จะมีความเร่งเฉพาะแกน ![]() เท่านั้นซึ่งเป็นค่าคงที่เท่ากับ
เท่านั้นซึ่งเป็นค่าคงที่เท่ากับ
![]() เช่นขว้างลูกบอลออกไปในแนวระดับเราสามารแยกพิจารณาเป็นการเคลื่อนที่ได้
2 แบบคือการเคลื่อนที่ในแนวราบด้วยความเร็วคงที่
เช่นขว้างลูกบอลออกไปในแนวระดับเราสามารแยกพิจารณาเป็นการเคลื่อนที่ได้
2 แบบคือการเคลื่อนที่ในแนวราบด้วยความเร็วคงที่ ![]() กับการเคลื่อนที่ในแนวดิ่ง
กับการเคลื่อนที่ในแนวดิ่ง
เป็นกานยากที่จะเขียนสูตรเกี่ยวกับการเคลื่อนที่แบบโปรเจกไตล์ในลักษณะต่าง
ๆ ได้อย่างครบถ้วน ตัวอย่างที่จะแสดงต่อไปนี้จะอาศัยการเคลื่อนที่ในแนวแกน ![]() และแนวแกน
และแนวแกน ![]() มาอธิบายถึงการเคลื่อนที่แบบโปรเจกไตล์
มาอธิบายถึงการเคลื่อนที่แบบโปรเจกไตล์
ตัวอย่างที่ 3.6 นักเบสบอลขว้างลูกบอลออกไปในแนวระดับด้วยความเร็ว 42.5 m ที่ระยะสูงจากพื้นดิน 2 m ดังรูปที่ 3.8
ก. เวลาที่ลูกบอลเคลื่อนที่ถึงคนรับลูกซึ่งอยู่ห่างจากคนขว้าง 18.5 m
ข. ลูกบอลจะอยู่สูงจากพื้นเท่าใด
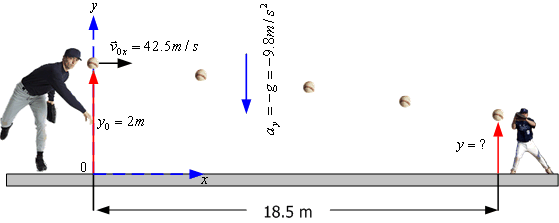
รูปที่ 3.8
วิธีทำ ตั้งแกนอ้างอิงที่พื้น (จุดเริ่มต้นไม่ได้อยู่ที่จุด 0,0) เมื่อ
ค่าตามแกน
![]()
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]()
ค่าตามแกน
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
ก. หาเวลาจากการเคลื่อนที่ในแนวแกน ![]()
![]() =
= ![]()
เนื่องจากเป็นการเคลื่อนที่แบบโปรเจกไตล์ความเร่งในแนวแกน ![]() เป็นศูนย์
เป็นศูนย์ ![]()
![]() จะได้
จะได้
![]() =
= ![]() =
= ![]()
= ![]()
ข. พิจารณาการเคลื่อนที่ในแนวแกน
![]() เมื่อความเร็วต้นในแนวแกน
เมื่อความเร็วต้นในแนวแกน ![]() เป็นศูนย์
เป็นศูนย์ ![]()
![]() =
= ![]()
แต่
![]()
![]() =
= ![]()
= ![]()
ตัวอย่างที่
3.7 ที่สนามเบสบอลแห่งหนึ่งฐานที่หนึ่งอยู่ห่างจากฐานที่สาม
![]() ผู้รักษาฐานที่สามขว้างลูกบอลออกไปด้วยความเร็ว
ผู้รักษาฐานที่สามขว้างลูกบอลออกไปด้วยความเร็ว
![]() ทำมุม
ทำมุม ![]() กับแนวระดับที่ความสูงเดียวกันไปยังฐานที่หนึ่ง
จงหามุม
กับแนวระดับที่ความสูงเดียวกันไปยังฐานที่หนึ่ง
จงหามุม ![]() ดังรูปที่ 3.9
ดังรูปที่ 3.9
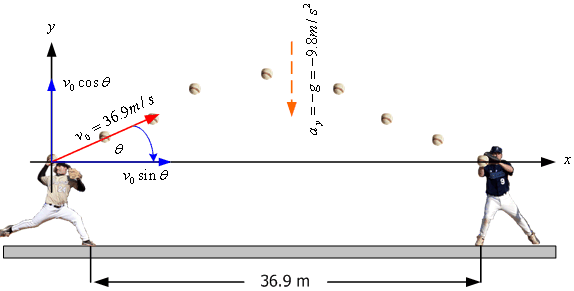
รูปที่ 3.9
วิธีทำ แกนอ้างอิงอยู่ที่มือคนขว้าง เมื่อ
ค่าตามแกน
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
ค่าตามแกน
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
พิจารณาการเคลื่อนที่ในแนวแกน
![]()
![]() =
= ![]()
เมื่อ
![]() ;
; ![]()
![]() =
= ![]()
![]() =
= ![]()
พิจารณาการเคลื่อนที่ในแนวแกน
![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
แทนค่า
![]() จากสมการข้างบน
จากสมการข้างบน
![]() =
= 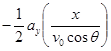
![]() =
= ![]()
แต่ ![]() จะได้
จะได้
![]() =
= ![]()
![]() =
= 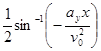
แทนค่าต่าง
ๆ ลงในสมการเมื่อ ![]()
![]() =
= 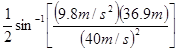
= ![]()
ตัวอย่างที่ 3.8 นายพรานเล็งปืนไปที่ลิงซึ่งเกาะอยู่ที่กิ่งไม้ ขณะที่นายพรานยิงปืนลิงก็ปล่อยมือจากกิ่งไม้พร้อมกัน ดังรูปที่ 3.10 จงแสดงให้เห็นว่านายพรานยิงปืนถูกลิง โดยไม่คำนึงถึงความเร็วต้น
วิธีทำ ให้ปากกระบอกปืนเป็นระดับอ้างอิง
ค่าต่าง
ๆ คิดที่ลิง (monkey) ค่าตามแกน ![]() ไม่มี มีเฉพาะค่าตามแกน
ไม่มี มีเฉพาะค่าตามแกน ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]()
ค่าต่าง ๆ คิดที่กระสุน (bullet)
ค่าตามแกน
![]()
![]() ,
, ![]() ;
; ![]() ;
;
![]()
ค่าตามแกน
![]()
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]()

รูปที่ 3.10
พิจารณาที่ลิงเมื่อลิงเคลื่อนที่ตามแนวดิ่ง
![]() =
= ![]()
![]() =
= ![]() ……(1)
……(1)
พิจารณาที่ลูกกระสุนแยกพิจารณาเป็น
การเคลื่อนที่ในแนวแกน
![]()
![]() =
= ![]()
= ![]()
![]() =
= ![]()
= ![]() …..(2)
…..(2)
การเคลื่อนที่ในแนวแกน ![]()
![]() =
= ![]()
![]() =
= ![]() .…(3)
.…(3)
แทนค่า
![]() จากสมการที่ (2) ลงในสมการที่ (3)
จากสมการที่ (2) ลงในสมการที่ (3)
![]() =
= 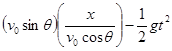
= ![]()
แต่
![]() ดังนั้นจะได้
ดังนั้นจะได้
![]() =
= ![]() =
= ![]()
นั่นคือกระสุนจะโดนลิง จะสังเกตุได้ง่ายในกรณีที่ไม่มีแรงโน้มถ่วงกระสุนจะยิงถูกลิงเหมือนกัน เนื่องจากทั้งลิงและกระสุนไม่มีแรงกระทำในแนวดิ่ง
3.3 การเคลื่อนที่เป็นวงกลมสม่ำเสมอ
พิจารณาการเคลื่อนที่แบบวงกลมสม่ำเสมอใน
2 มิติ การเคลื่อนที่แบบวงกลมหมายถึง ![]() สม่ำเสมอหมายถึง
สม่ำเสมอหมายถึง ![]() ในที่นี่จะกล่าวถึงการเคลื่อนที่แบบวงกลมด้วยความเร็วคงที่
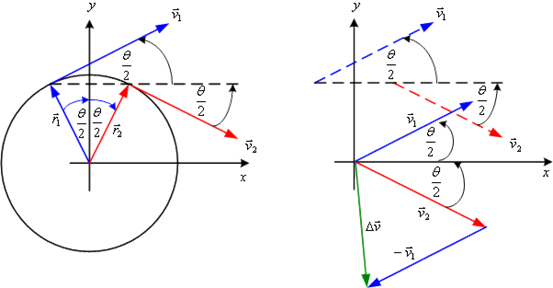
พิจารณาความเร่งของปลายเข็มทั้งสองของเข็มนาฬิกาในตัวอย่างที่ 3.4 ดังรูปที่ 3.11 ก. เมื่อเวกเตอร์ความเร็วคือเส้นสัมผัสวงกลมที่จุดใด
ๆ ดังนั้น
ความเร็วเริ่มต้นและความเร็วสุดท้ายสามารถเขียนอยู่ในรูปของเวกเตอร์ได้ดังรูป 3.11
ข. จะได้ส่วนประกอบในระบบพิกัดฉากของความเร็วต้น
ในที่นี่จะกล่าวถึงการเคลื่อนที่แบบวงกลมด้วยความเร็วคงที่
พิจารณาความเร่งของปลายเข็มทั้งสองของเข็มนาฬิกาในตัวอย่างที่ 3.4 ดังรูปที่ 3.11 ก. เมื่อเวกเตอร์ความเร็วคือเส้นสัมผัสวงกลมที่จุดใด
ๆ ดังนั้น
ความเร็วเริ่มต้นและความเร็วสุดท้ายสามารถเขียนอยู่ในรูปของเวกเตอร์ได้ดังรูป 3.11
ข. จะได้ส่วนประกอบในระบบพิกัดฉากของความเร็วต้น
![]() และความสุดท้าย
และความสุดท้าย ![]() คือ
คือ

รูปที่ 3.11 ก. รูปที่ 3.11 ข.
![]() =
= ![]()
และ ![]() =
= ![]()
เมื่อ
![]() คืออัตราเร็วของปลายเข็มทั้งสอง ดังนั้นการเปลี่ยนแปลงความเร็วคือ
คืออัตราเร็วของปลายเข็มทั้งสอง ดังนั้นการเปลี่ยนแปลงความเร็วคือ
![]() =
= ![]()
= ![]()
![]()
= ![]()
ถ้า
![]() มีค่าน้อยมาก ๆ
มีค่าน้อยมาก ๆ ![]()
![]() =
= ![]()
จะได้ ![]() =
= ![]()
จากนิยามความเร่ง ![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
นั่นคือความเร็วจะคงที่ แต่ความเร่งมีทิศสู่ศูนย์กลางเรียกว่า "ความเร่งสู่ศูนย์กลาง "
แทนด้วย
![]()
![]() =
= ![]()
วัตถุยังคงเคลื่อนที่แบบวงกลมสม่ำเสมอ แต่ความเร่งมีทิศเข้าสู่ศูนย์กลางโดยมีขนาดคงที่
ตัวอย่างที่ 3.9 จงหา ก. ความเร็ว ข. ความเร่ง ของคนที่ยืนอยู่ที่จุดศูนย์สูตร
วิธีทำ ก. ความเร็วคือระยะทางที่เคลื่อนที่ต่อเวลา
![]() =
= ![]() =
= ![]()
= ![]()
= ![]()
ข. ความเร่งที่เกิดขึ้นคือความเร่งสู่ศูนย์กลาง
![]() =
= ![]() =
= ![]()
= ![]()
การหาสมการความเร่ง ความเร็ว และตำแหน่งเป็นฟังก์ชั่นของเวลา และ
ความเร่ง ความเร็ว เป็นฟังก์ชั่นของตำแหน่งของวัตถุเมื่อเคลื่อนที่เป็นวงกลมสม่ำเสมอ
ดังรูปที่ 3.12 เริ่มต้นวัตถุอยู่บนแกน ![]() มีความเร็ว
มีความเร็ว ![]() ทิศตามแกน
ทิศตามแกน ![]() เมื่อเคลื่อนที่ครบ 1 รอบ จะได้สมการเคลื่อนที่
เมื่อเคลื่อนที่ครบ 1 รอบ จะได้สมการเคลื่อนที่

รูปที่ 3.12
![]() =
= ![]() =
= ![]() =
= ![]()
ค่าที่ได้เกิดจากการกวาดของมุมเมื่อเกิดการหมุนเรียกว่า " ความถี่เชิงมุม "
การกระจัดเชิงมุมเมื่อเขียนอยู่ในรูปฟังก์ชั่นของเวลา
![]() =
= ![]()
![]() =
= ![]()
= ![]()
![]() =
= ![]()
ความเร็วเขียนอยู่ในเทอมของความเร็วเชิงมุมได้ดังนี้
![]() =
= ![]() =
= ![]()
= ![]()
และ ![]() =
= ![]() =
= ![]()
= ![]()
ความเร่งเขียนอยู่ในรูปของเวกเตอร์เมื่อเป็นฟังก์ชั่นของเวลาเขียนได้เป็น
![]() =
= ![]()
= ![]()
พิจารณาความเร่งในแนวแกน
![]() ก่อน
ก่อน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
อินทิเกรตทั้งสองข้างโดยให้
![]() และ
และ ![]() เป็นค่าคงที่
เป็นค่าคงที่
![]() =
= 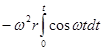
![]() =
= ![]()
= ![]()
จากนิยามของความเร็วสามารถหาตำแหน่งบนแกน
![]() ได้ดังนี้
ได้ดังนี้
![]() =
= ![]()
= ![]()
![]() =
= ![]()
อินทิเกรตทั้งสองข้าง
![]() =
= 
![]() =
= ![]()
= ![]()
![]() =
= ![]()
จากสมการความเร่งซึ่งเป็นฟังก์ชั่นของเวลา
![]() =
= ![]()
= ![]()
จากสมการความเร็วซึ่งเป็นฟังก์ชั่นของเวลา
![]() ยกกำลังสองทั้งสองข้างจะได้
ยกกำลังสองทั้งสองข้างจะได้
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
นั่นคือความเร็วมี 2 ขึ้นอยู่กับพิกัดการเคลื่อนที่
พิจารณาความเร่งในแนวแกน ![]() ในทำนองเดียวกับแกน
ในทำนองเดียวกับแกน ![]() จากสมการข้างต้นจะได้ว่า
จากสมการข้างต้นจะได้ว่า
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ตัวอย่างที่
3.1 จากรูปที่
3.13 ที่เวลา ![]() ดวงจันทร์อยู่บนแกน
ดวงจันทร์อยู่บนแกน ![]() เมื่อเวลาผ่านไปดวงจันทร์เคลื่อนที่ดังรูปที่
3.13 จงหา
เมื่อเวลาผ่านไปดวงจันทร์เคลื่อนที่ดังรูปที่
3.13 จงหา
ก. ความถี่เชิงมุมเมื่อดวงจันทร์อยู่ที่ตำแหน่งดังรูปที่ 3.13 จงหา
ข. ความเร็ว
ค. ความเร่ง
ง. เวลา
กำหนดให้
ดวงจันทร์มีรัศมีโคจร ![]() และ คาบการโคจร
และ คาบการโคจร ![]()

รูปที่ 3.13
วิธีทำ ก. ![]() =
= ![]() =
= ![]()
= ![]()
จากรูปจะได้ส่วนประกอบเวกเตอร์ตำแหน่งบนแกน
![]() และ
และ ![]() คือ
คือ
![]() และ
และ
![]()
ข. องค์ประกอบความเร็ว ณ. ตำแหน่งดังรูปหาได้ดังนี้
![]() =
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ดังนั้นความเร็ว ณ. ตำแหน่งดังกล่าวคือ
![]()
ค. องค์ประกอบความเร่ง ณ. ตำแหน่งดังรูป
![]() =
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ดังนั้นความเร่ง
ณ. ตำแหน่งดังกล่าวคือ ![]()
ง. พิจารณาตำแหน่งที่เป็นฟังก์ชั่นของเวลา
![]() =
= ![]()
แต่
![]() (จากโจทย์
(จากโจทย์ ![]() )
)
![]() =
= 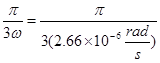
= ![]()
= ![]()
สรุป
นิยามตำแหน่ง
: ![]()
นิยามการกระจัด
: ![]()
นิยามความเร็ว
: ![]()
นิยามอัตราเร็ว
: ![]()
นิยามความเร่ง
: ![]()
การเคลื่อนที่แบบโปรเจกไตล์ ความเร่งในแนวแกน
![]() เป็นศูนย์
สามารถแยกพิจารณาในแต่ละแกนได้โดยใช้สมการการเคลื่อนที่เมื่อความเร่งคงที่
เป็นศูนย์
สามารถแยกพิจารณาในแต่ละแกนได้โดยใช้สมการการเคลื่อนที่เมื่อความเร่งคงที่
การเคลื่อนที่เป็นวงกลม ความเร่งจะมีทิศเข้าสู่ศูนย์กลาง
ความเร่งสู่ศูนย์กลาง : ![]()